//
Search
🌉

[0] Schrödinger Bridge Overview

Diffusion Series
Diffusion Theory Summary
Image-to-image Translation
EGSDE: Unpaired I2I Translation via Energy-Guided SDEs.
SDDM: Score-Decomposed Diffusion Models on Manifolds for Unpaired I2I Translation
Schrodinger Bridge Series
[0] Schrödinger Bridge Overview
[21NeurIPS] DSB: Schrödinger Bridge
[23CVPR] BBDM: Image-to-image Translation with Brownian Bridge Diffusion Models
요즘 Diffusion 필드에서 슈뢰딩거 다리 (SCHRÖDINGER BRIDGE)가 새로운 트렌드로 떠오르는 것 같다. 관련 논문이 많이 나오길래, 따라잡아보았다.

최근 연구 동향

21ICML DGLSB: Deep generative learning via schrödinger bridge [code]
•
Developed a two-stage unsupervised procedure for estimating the SB between a Dirac delta and data.
21NeurIPS DSB: Diffusion Schrödinger Bridge with Applications to Score-Based Generative Modeling. [code]
•
Extends the Iterative Proportional Fitting (IPF) procedure to the continuous setting.
22arXiv RSB: Applying Regularized Schrödinger-Bridge-Based Stochastic Process in Generative Modeling. [code]
22UAI CSB: Conditional Simulation Using Diffusion Schrödinger Bridges [code]
22ICLR SB-FBSDE: Likelihood Training of Schrödinger Bridge using Forward-Backward SDEs Theory.
•
proposes likelihood training of SBs using Forward-Backward SDEs theory. [code]
23arXiv Conditional flow matching: Simulation-free dynamic optimal transport. [code]
•
Solves the SB problem with a conditional variant of flow matching.
23ICML [SF]2M: Simulation-free Schrödinger bridges via score and flow matching [code]
23ICMLw OT-CFM: Improving and generalizing flow-based generative models with minibatch optimal transport [code]

Applications

23arXiv InDI: Inversion by direct iteration: An alternative to denoising diffusion for image restoration.
•
Uses paired data to learn SBs between Dirac delta and data
•
Discovered DDIMs as SBs between data and Gaussian distributions.
23arXiv UNSB: Unpaired Neural Schrödinger Bridge [code]

1. Prelinamary: SGMs (score-based generative modeling)

•
생성 모델링 (Generative Modeling)에서는 주어진 분포 ppriorp_{\mathrm{prior}} 를 주어진 데이터 분포 pdatap_{\mathrm{data}} 로 변환 (Transform)하는 알고리즘을 설계하는데 관심이 있습니다. 데이터 분포 pdatap_{\mathrm{data}} 는 샘플을 통해서만 접근할 수 있습니다.
•
Energy-based Models, GANs, Normalizing Flow, VAE 또는 Diffusion Score-matching 과 같은 다양한 프레임워크가 연구되어왔습니다.
•
Diffusion Model은 시각적 품질 측면에서 GAN을 능가하는 데 큰 가능성을 보여주었으며, 확산 과정의 이산화(discretization)로 재구성 될 수 있으므로 수학적 관점에서도 매력적입니다.
•
Score-based Generative Modeling: Yang Song의 블로그 게시물이나 논문 [2,3]을 참고하세요.
SGMs
1차원 Standard Wiener Process
•
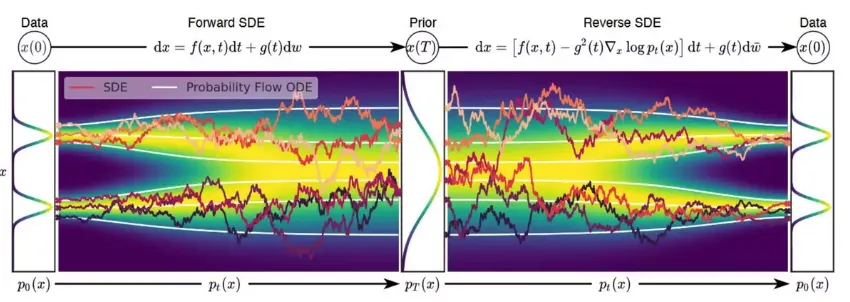
SGM: 확산 과정이 시간에 따라 연속적일 때 확률적 미분 방정식(SDE)으로 표현할 수 있습니다 [Song 19]
•
Forward Process (데이터분포→ 사전분포)
dxt=f(xt,t)dt+g(t)dwt,x0∼pdata \begin{equation}\mathrm{d} \boldsymbol{x}_t=\boldsymbol{f}\left(\boldsymbol{x}_t, t\right) \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t, \quad \boldsymbol{x}_0 \sim p_{\text {data }}\end{equation}
•
f\boldsymbol{f} (벡터 함수): 드리프트 계수 gg (스칼라 함수): 는 확산 계수 wt\boldsymbol{w}_t: Standard Wiener Process (Standard Brownian Motion) → 평균이 0인 분산의 정규 분포 t를 따르는 연속 확률 변수.
•
Reverse Process (사전분포 → 데이터분포)
dxt=[f(xt,t)−g2(t)∇log⁡pt(xt)]dt+g(t)dwt,xT∼pprior \begin{equation}\mathrm{d} \boldsymbol{x}_t=\left[\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)-g^2(t) \nabla \log p_t\left(\boldsymbol{x}_t\right)\right] \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t, \quad \boldsymbol{x}_T \sim p_{\text {prior }}\end{equation}
•
드리프트 계수에 Score Function ∇log⁡pt(xt)\nabla \log p_t\left(\boldsymbol{x}_t\right) 항이 추가되었습니다.
•
함수 p(t)p(t) 는 확률 밀도 뒤에 순방향 과정에서 xtx_t 가 됩니다. (xt∼pt(x)x_t\sim p_t(x)).
◦
이때, pt:=p(⋅;t).p_t:=p(\cdot;t).
•
Forward Process에서 확률분포 ptp_t 다음 xtx_t가 오는 것은 Fokker-Plank (FP) 방정식으로 주어집니다.
◦
Kolmogorov's equation of advance 라고도 함.
◦
Forward Process (1) 에 대응하는 FP는 다음과 같이 주어짐.
◦
p0(x)=pdata(x)p_0(x)=p_{data}(x)는 명시적이지 않으므로 솔루션이 존재하지 않음.
∂∂tpt(x)=−∇⋅[f(x,t)pt(x)]+12g2(t)Δpt(x)\begin{equation} \frac{\partial}{\partial t} p_t(\boldsymbol{x})=-\nabla \cdot\left[\boldsymbol{f}(\boldsymbol{x}, t) p_t(\boldsymbol{x})\right]+\frac{1}{2} g^2(t) \Delta p_t(\boldsymbol{x}) \end{equation}
•
Objective Parameter화 된 모델 sθ(x,t)s_\theta(x,t)에 대해 ∇log⁡pt(x)\nabla \log p_t(x)를 학습합니다.
◦
생성( 회귀프로세스) 중에는 밀도함수 pt(x)p_t(x)를 알 필요가 없음.
◦
조건부 확률 pt(xt∣x0)p_t(x_t|x_0)의 score에 대한 L2 Loss 최소화
θ∗=argmin⁡θEt,x0,xt∣x0λ(t)∥sθ(xt,t)−∇log⁡pt(xt∣x0)∥2\begin{equation}\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\operatorname{argmin}} \mathbb{E}_{t, \boldsymbol{x}_0, \boldsymbol{x}_t \mid \boldsymbol{x}_0} \lambda(t)\left\|\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)-\nabla \log p_t\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)\right\|^2\end{equation}
•
Score-Matching 위 손실함수는 다음 최적화문제와 동일합니다.
θ∗=argmin⁡θEt,xtλ(t)∥sθ(xt,t)−∇log⁡pt(xt)∥2\begin{equation}\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\operatorname{argmin}} \mathbb{E}_{t, \orange{\boldsymbol{x}_t}} \lambda(t)\left\|\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)-\nabla \log \orange{p_t\left({\boldsymbol{x}_t}\right)}\right\|^2\end{equation}
•
학습된 score 추정모델 sθ∗s_{\theta^*}를 사용해 회귀프로세스의 해 x0x_0를 구합니다.
•
정확도 및 계산복잡성을 고려하여 다양한 알고리즘을 사용합니다.
dxt=[f(xt,t)−g2(t)sθ∗(xt,t)]dt+g(t)dwt,xT∼pprior \begin{equation}\mathrm{d} \boldsymbol{x}_t=\left[\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)-g^2(t) \boldsymbol{s}_{\boldsymbol{\theta}^*}\left(\boldsymbol{x}_t, t\right)\right] \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t, \quad \boldsymbol{x}_T \sim p_{\text {prior }}\end{equation}
•
가장 간단한 솔루션은 Euler-maruyama method입니다.
◦
상미분방정식 (ODE)에 대한 수치 솔루션인 오일러 방법의 SDE 버전.
xk−1=xk−[f(xk,tk)−g2(tk)sθ∗(xk,tk)]Δtk+g(tk)Δtkzk,zk∼N(0,I)\begin{equation}\boldsymbol{x}_{k-1}=\boldsymbol{x}_k-\left[\boldsymbol{f}\left(\boldsymbol{x}_k, t_k\right)-g^2\left(t_k\right) \boldsymbol{s}_{\boldsymbol{\theta}^*}\left(\boldsymbol{x}_k, t_k\right)\right] \Delta t_k+g\left(t_k\right) \sqrt{\Delta t_k}\boldsymbol{z}_k, \quad \boldsymbol{z}_k \sim N(\mathbf{0}, \boldsymbol{I})\end{equation}
•
이는 오일러 방법에 노이즈항이 추가된 형태입니다. (DDPM과 동일)

ODE (Probability Flow ODE)

•
실제로 확산 모델의 많은 응용 분야에서는 생성에 SDE 대신 ODE를 사용합니다.
•
확산 모델의 SDE는 Probability Flow ODE → 공통 밀도 함수를 가진 ODE를 동반합니다.
Probability Flow ODE:dxt=[f(xt,t)−g2(t)∇log⁡pt(xt)]dt+g(t)dwtStochastic Flow SDE: dxt=[f(xt,t)−12g2(t)∇log⁡pt(xt)]dt\begin{align} \text{Probability Flow ODE:}\quad&\mathrm{d} \boldsymbol{x}_t=\left[\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)-g^2(t) \nabla \log p_t\left(\boldsymbol{x}_t\right)\right] \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t \\ \text{Stochastic Flow SDE:}\quad&\mathrm{~d} \boldsymbol{x}_t=\left[\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)-\frac{1}{2} g^2(t) \nabla \log p_t\left(\boldsymbol{x}_t\right)\right] \mathrm{d} t \end{align}
•
장점:
1.
재학습 없이 기존 학습된 모델에 적용 가능
2.
결정론적 생성 과정이기 때문에 고정된 초기값에 대해 항상 동일한 결과를 보장됨.
3.
오랫동안 연구된 ODE Solver를 사용할 수 있음. (예: Runge-Kutta 방법)
•
SDE → Probability Flow ODE 유도
1.
Δp=∇⋅(∇p)=∇⋅(p∇log⁡p)\Delta p=\nabla \cdot(\nabla p)=\nabla \cdot(p \nabla \log p)를 FP방정식에 적용 (로그 미분 공식)
2.
변수변환 f~:=f−1/2⋅g2∇log⁡p\tilde{\boldsymbol{f}}:=\boldsymbol{f}-1 / 2 \cdot g^2 \nabla \log p 은 확산항이 없는 FP방정식이고 해는 Forward Porcess와 일치.
3.
변환된 FP방정식에 해당하는 (확률) 미분방정식 중 하나는 Probability Flow ODE.
∂p∂t=−∇⋅[fp]+12g2Δp=−∇⋅[(f−12g2∇log⁡p)p]=−∇⋅[f~p]\frac{\partial p}{\partial t}=-\nabla \cdot[\boldsymbol{f} p]+\frac{1}{2} g^2 \Delta p=-\nabla \cdot\left[\left(\boldsymbol{f}-\frac{1}{2} g^2 \nabla \log p\right) p\right]=-\nabla \cdot[\tilde{\boldsymbol{f}} p]
FP SDE와 Probability Flow ODE
Generative model for CelebA. from Yang Song Blog.
점수 기반 생성 모델링의 주요 한계 중 하나는 초기 forward process가 ppriorp_{\text{prior}}에 근접하도록 많은 양의 step를 요구하고 신경망 근사가 유지되도록 충분히 작은 크기의 stepsize를 요구한다는 것입니다.
이를 해결하기 위해 Diffusion Schrödinger Bridge가 제안되었습니다.
•
기존 Score-based Modeling의 일반화 버전.
•
Score-based 방법에 비해 필요한 stepsize의 수를 크게 줄일 수 있음.
•
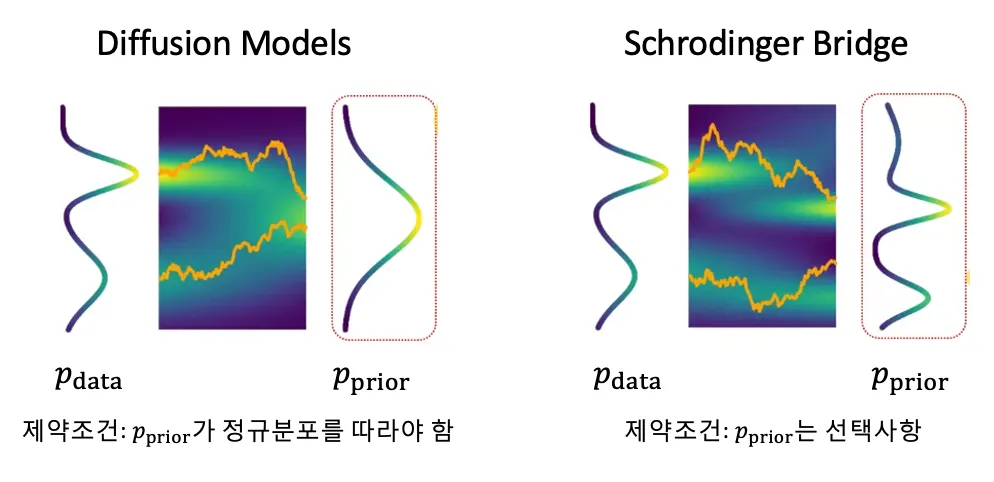
ppriorp_{\text{prior}}가 Gaussian이어야 한다는 제한을 제거함
•
따라서 고차원 최적 운송 (Optimal Transport) 에 대한 가능성을 열음.

Schrodinger Bridge - “진정한” Image-to-image를 향하여

•
Diffusion Models의 체계를 Image-to-image로 확장하려고 합니다.
•
하지만 입력 이미지는 guide가 아닌 다른 방법으로 간주합니다.
•
사전확률분포를 임의의 분포로 대체하지 않는 이유? → Forward Process의 설계 방법이 문제가 됩니다.
◦
확률 밀도에 대한 pT≈ppriorp_T\approx p_{prior}를 만족하기 위해 하이퍼파라메터 f,g\boldsymbol{f},g를 설계해야 함 (FP방정식에서 pTp_T는 p0,f,gp_0, \boldsymbol{f},g에 의해 자동으로 결정됨)
◦
하지만 일반적으로 pdata,ppriorp_{data}, p_{prior}는 암시적이므로 학습전에 설계된 f,g\boldsymbol{f},g를 사용하기 어려움.
•
확산 모델에 대한 FP 방정식은 다음과 같습니다.
∂∂tpt(x)=−∇⋅[f(x,t)pt(x)]+12g2(t)Δpt(x),p0=pdata \frac{\partial}{\partial t} p_t(\boldsymbol{x})=-\nabla \cdot\left[\boldsymbol{f}(\boldsymbol{x}, t) p_t(\boldsymbol{x})\right]+\frac{1}{2} g^2(t) \Delta p_t(\boldsymbol{x}), \quad \orange{p_0=p_{\text {data }}}
•
확산 모델 대신 조금 더 추상화된 생성모델에 대한 문제 설정을 고려하겠습니다.
1.
데이터분포 pdatap_{data}와 사전분포 ppriorp_{prior}가 주어지면,
2.
각 분포는 SDE를 통해 연결됩니다.
3.
SDE에 따라 확률밀도 pt(x)p_t(x)를 모델링합니다. (경계조건: p0=pdata,pT=pprior)p_0=p_{data}, p_{T}=p_{prior})
•
Schrodinger Bridge
•
분포는 브라운 운동 사이의 “다리”가 됩니다.
•
양자역학의 슈뢰딩거 방정식과는 다릅니다. (관련은 있습니다.)
•
C. Léonard (2013), Y. Chen et al. (2020)

Dynamic Schrodinger Bridge (Static SB)

•
SB는 확률 과정의 경로 측도 제약이있는 KL 다이버전스 최소화 문제로 공식화
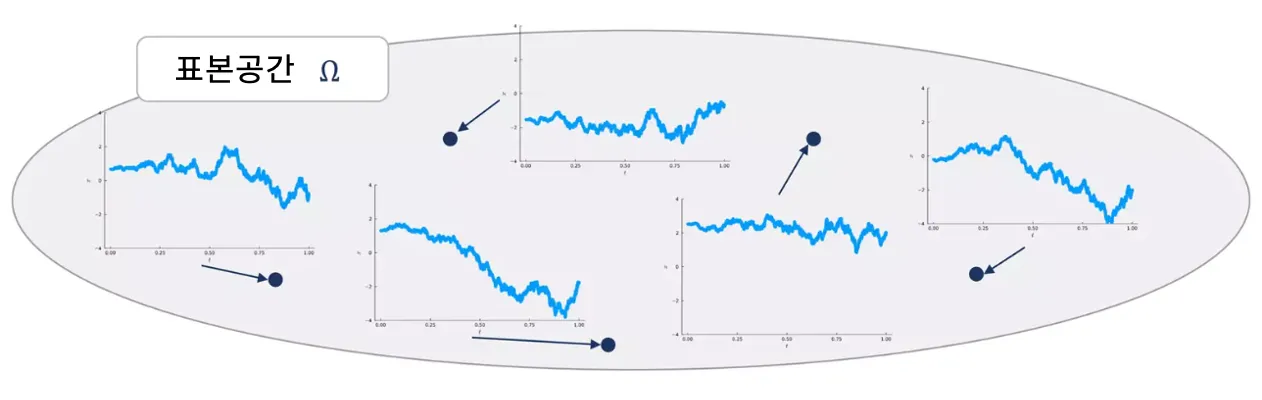
min⁡PDKL(P∥Q)s.t.P0=μdata ,PT=μprior \begin{equation} \min _{\mathbb{P}} D_{\mathrm{KL}}(\mathbb{P} \| \mathbb{Q}) \quad \text{s.t.}\quad \mathbb{P}_0=\mu_{\text {data }}, \mathbb{P}_T=\mu_{\text {prior }} \end{equation}
•
경로 측도는 경로 xt≤t≤Tx_t \leq t \leq T 전체를 하나의 단일표본으로 보았을 때의 확률분포에 해당합니다.
•
여기서, 경로 측도 ℙ, ℚ는 각각 근사 분포와 참 분포에 대응하며, 특히 ℚ를 참조측도라 부릅니다.
•
후술하는 static SB와 대비하여, 이는 dynamic SB라고도 불립니다.

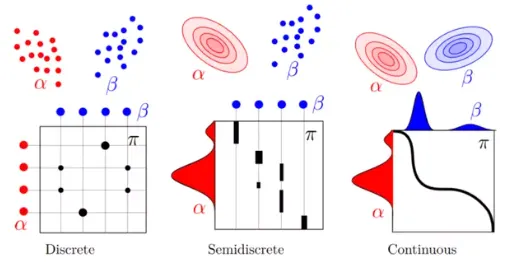
Static Schrodinger Bridge (Static SB)

π.α.β는 각각 ℙ0,𝑇, 𝜇0, 𝜇𝑇에 대응
•
Dynamic SB의 최적해는 관련된 Static SB의 해로 구성할 수 있습니다.
◦
완만한 가정 하에서 양자의 최적해는 일대일로 대응합니다. (후술)
•
Static SB: 처음 및 마지막 시간에 대한 결합분포에 대한 KL Divergence 최소화 문제.
◦
도중의 경로를 주변화 (Marginalize)해 시점과 종점의 조합만을 고려하는 설정
min⁡P0,TDKL(P0,T∥Q0,T)s.t.P0=μ0,PT=μT\begin{equation}\min _{\mathbb{P}_{0, T}} D_{\mathrm{KL}}\left(\mathbb{P}_{0, T} \| \mathbb{Q}_{0, T}\right) \quad\text{s.t.}\quad \mathbb{P}_0=\mu_0, \quad \mathbb{P}_T=\mu_T\end{equation}

Dynamic SB와 Static SB의 관계

•
Dynamic SB의 해를 P∗\mathbb{P}^*, static SB의 해를 P0,T∗\mathbb{P}_{0, T}^* 로 나타냅니다.
•
P∗\mathbb{P}^* 는 참조 diffusion bridge Q∣0,T\mathbb{Q}_{|0,T}의 주변화로 주어집니다. [Leonard 13]
◦
양단의 값 (x0,xT)(x_0,x_T)이 고정된 확산과정을 (Diffusion) Bridge라고 부릅니다.
◦
P∗\mathbb{P}^*와 같이 bridge의 주변화로 구성된 경로 측도를 Mixture of bridges라고 부릅니다.
◦
또한 반대로 P0,T∗\mathbb{P}^*_{0,T}를 P∗\mathbb{P}^*에서 고유하게 구성할 수 있습니다.
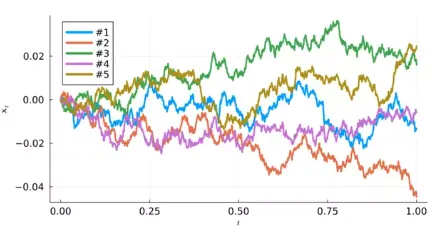
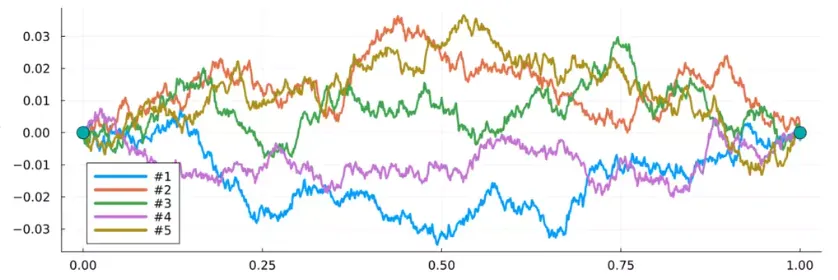
P∗(⋅)=∫Q∣0,T(⋅∣x0,xT)dP0,T∗(x0,xT)\begin{equation}\mathbb{P}^*(\cdot)=\int \mathbb{Q}_{\mid 0, T}\left(\cdot \mid \boldsymbol{x}_0, \boldsymbol{x}_T\right) \mathrm{d} \mathbb{P}_{0, T}^*\left(\boldsymbol{x}_0, \boldsymbol{x}_T\right)\end{equation}
1차원Diffusion Bridge Q∣0,T(⋅∣x0=0,xT=0)\mathbb{Q}_{\mid 0, T}\left(\cdot \mid \boldsymbol{x}_0=0, \boldsymbol{x}_T=0\right) 의 표본 경로

최적 수송 (Optimal Transport; OT)

•
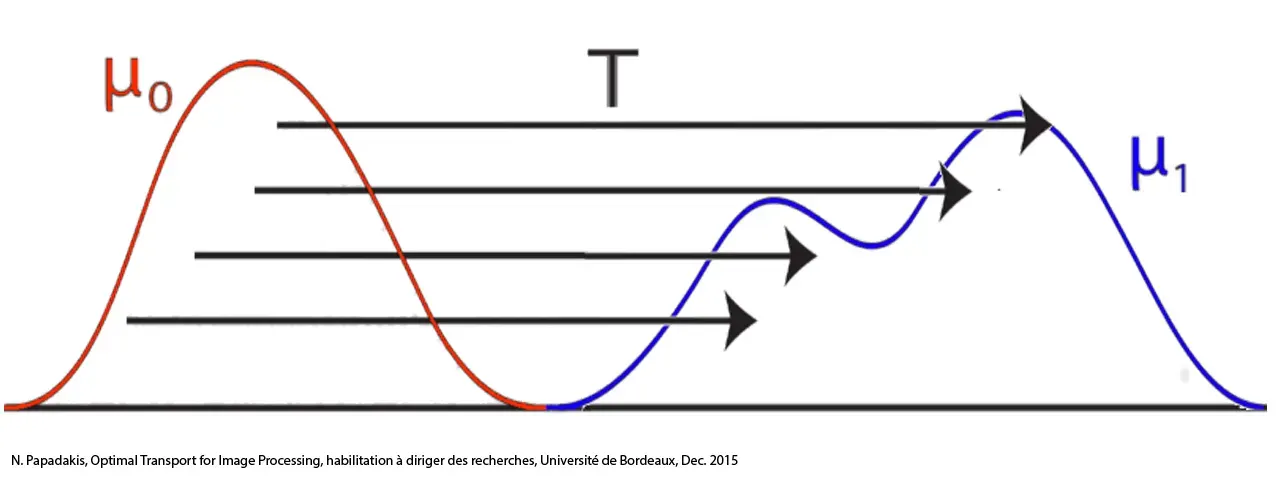
Optimal Transport: 확률분포를 이동 시킬 때 비용을 최소화 하는 운반방법을 찾는 문제
•
어떤 종류의 조건 하에서 (static) SB는 최적 수송과 같은 것으로 알려져 있습니다. [Leonard 13]
•
밀도 함수를 모래 산으로 보고, 한 모래산을 운반하여 다른 형태의 모래산을 구축할 때 걸리는 운반비용 (거리와 운반량에 상관)이 최소가 되는 조합을 찾는 문제

Kantorovich Optimal Transport

•
현대적인 최적수송의 공식화는 Kantorovich의 방법을 사용합니다.
•
총 이동 비용을 최소화하는 커플링 측도 𝜋 를 찾는 문제로 볼 수 있습니다.
◦
한 점에서 다른 점으로 이동할 때 분할 및 통합을 인정하는 설정
◦
수송원, 수송처의 확률 측도를 각각 𝛼, 𝛽로 표기
◦
여기서 단위 질량의 좌표 x∈X\boldsymbol{x}\in\mathcal{X} 에서 y∈Y\boldsymbol{y}\in\mathcal{Y} 로의 이동 비용을 𝑐(𝒙, 𝒚)로 정의 [Peyre 20]
min⁡π∫X×Yc(x,y)dπ(x,y) s.t. π(⋅×Y)=α,π(X×⋅)=β\begin{equation} \min _\pi \int_{\mathcal{X} \times \mathcal{Y}} c(\boldsymbol{x}, \boldsymbol{y}) \mathrm{d} \pi(\boldsymbol{x}, \boldsymbol{y}) \quad \text { s.t. } \quad \pi(\cdot \times \mathcal{Y})=\alpha, \quad \pi(X \times \cdot)=\beta \end{equation}

엔트로피 정규화 OT (Entory-Regularized OT; EROT)

•
수치 계산으로 OT를 취급할 때는 엔트로피 정규화를 더한 완화 문제를 생각하는 경우가 많습니다.
•
비용 함수가 𝜋에 관해 강볼록하게 되므로, 최적해가 고유하게 정해져서 수치계산이 편합니다.
•
원래 OT는 볼록하지만 일반적으로 강볼록하지 않기 때문에 최적해는 고유하지 않습니다.
min⁡π∫X×Yc(x,y)dπ(x,y)+εH(π) s.t. π(⋅×Y)=α,π(X×⋅)=βH(π):=−∫x×yp(x,y)log⁡p(x,y)dxdy\begin{equation} \begin{gathered} \min _\pi \int_{\mathcal{X} \times \mathcal{Y}} c(\boldsymbol{x}, \boldsymbol{y}) \mathrm{d} \pi(\boldsymbol{x}, \boldsymbol{y})\orange{+\varepsilon H(\pi)} \quad\text { s.t. } \pi(\cdot \times \mathcal{Y})=\alpha, \quad \pi(X \times \cdot)=\beta \\ H(\pi):=-\int_{x \times y} p(\boldsymbol{x}, \boldsymbol{y}) \log p(\boldsymbol{x}, \boldsymbol{y}) \mathrm{d} \boldsymbol{x} \mathrm{d} \boldsymbol{y}\end{gathered}\end{equation}
•
여기서 H(π)H(\pi)는 미분 엔트로피.
•
식 (14)에서는 측도 𝜋에 대응하는 밀도함수 p(x,y)p(x,y)가 존재한다고 가정합니다.
•
보다 엄밀하게는, 이산 OT와의 대응을 고려하여 상대 엔트로피[Peyre 20]로 정의하는 것이 바람직합니다.

SB와 OT의 관계

•
기준 측도가 가역 Brown 운동일 때, static SB 와 EROT 는 최적해가 일치합니다. [Chen 20][Peyre 20]
◦
정상적인 주변 측도를 가지는 Brown 운동을 가역 Brown 운동이라고 부릅니다. (Qt=Qs∀0≤t≤s≤T)\left(\mathbb{Q}_t=\mathbb{Q}_s \forall 0 \leq t \leq s \leq T\right)
◦
가역 Brown 운동이라면 거리 함수가 존재합니다: q0,T(x0,xT)∝exp⁡[−c(x0,xT)]q_{0, T}\left(\boldsymbol{x}_0, \boldsymbol{x}_T\right) \propto \exp \left[-c\left(\boldsymbol{x}_0, \boldsymbol{x}_T\right)\right]
◦
예를들어 정의 영역이 Euclid 공간 Rn\mathbb{R}^n 일때 가역 Brown 운동 Q\mathbb{Q} 에 관련된 SDE는 dxt=σdwt\mathrm{d} \boldsymbol{x}_t=\sigma \mathrm{d} \boldsymbol{w}_t이며, 거리 함수는 제곱 Euclid의 Norm: c(x0,xT)=∥x0−xT∥2/2σ2c\left(\boldsymbol{x}_0, \boldsymbol{x}_T\right)=\left\|\boldsymbol{x}_0-\boldsymbol{x}_T\right\|^2 / 2 \sigma^2
•
확률 밀도 함수가 존재할 때의 증명은 다음과 같습니다.
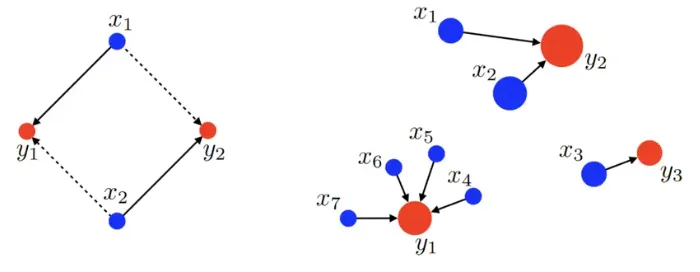
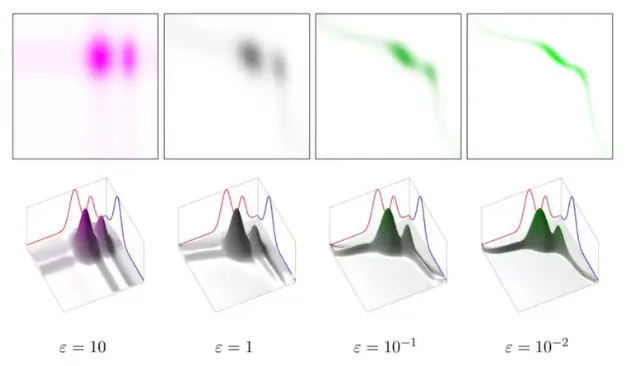
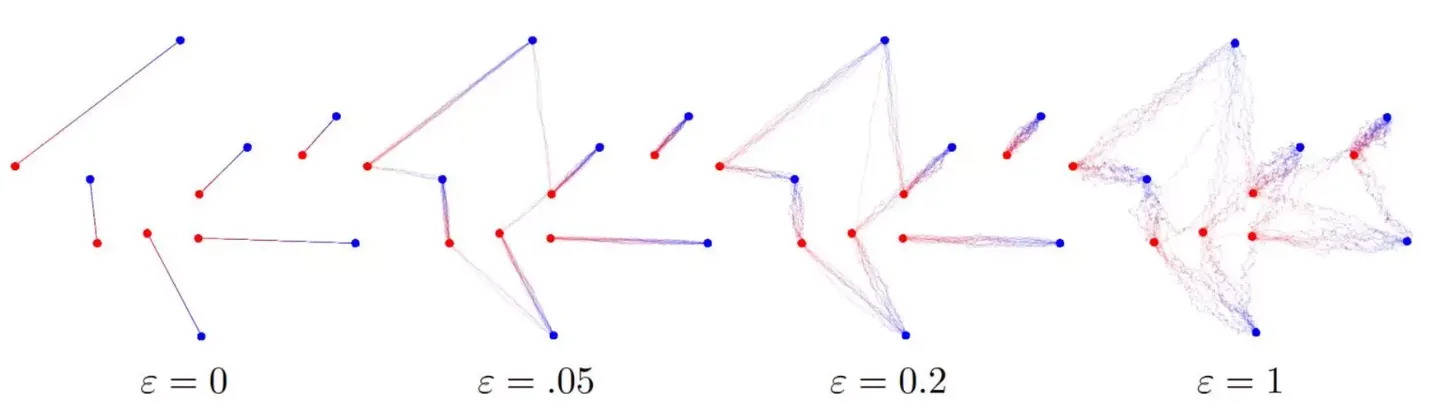
DKL(P0,T∥Q0,T)=−EP0,T[log⁡q0,T]+EP0,T[log⁡p0,T]=−EP0,T[−c(x0,xT)]+H(P0,T)+ const. =∫c(x0,xT)dP0,T(x0,xT)+H(P0,T)+ const. \begin{equation}\begin{aligned}D_{\mathrm{KL}}\left(\mathbb{P}_{0, T} \| \mathbb{Q}_{0, T}\right) & =-\mathbb{E}_{\mathbb{P}_{0, T}}\left[\log q_{0, T}\right]+\mathbb{E}_{\mathbb{P}_{0, T}}\left[\log p_{0, T}\right] \\& =-\mathbb{E}_{\mathbb{P}_{0, T}}\left[-c\left(\boldsymbol{x}_0, \boldsymbol{x}_T\right)\right]+H\left(\mathbb{P}_{0, T}\right)+\text { const. } \\& =\int c\left(\boldsymbol{x}_0, \boldsymbol{x}_T\right) \mathrm{d} \mathbb{P}_{0, T}\left(\boldsymbol{x}_0, \boldsymbol{x}_T\right)+H\left(\mathbb{P}_{0, T}\right)+\text { const. }\end{aligned}\end{equation}
이산 EROT의 해로 구성된 mixture of bridges
•
파란색 점들로부터 빨간색 점들로의 수송 경로 (각 점의 질량은 모두 동일하다고 가정)
•
엔트로피항의 기여(𝜀) 가 커질수록 허용 가능한 bridge가 다양화되는 경향을 보입니다.

SB 재정의: 확률 최적 제어 문제

•
패스 측도는 그대로라면 다루기 어려우므로 SDE를 이용한 표현으로 바꾸기로 합니다.
◦
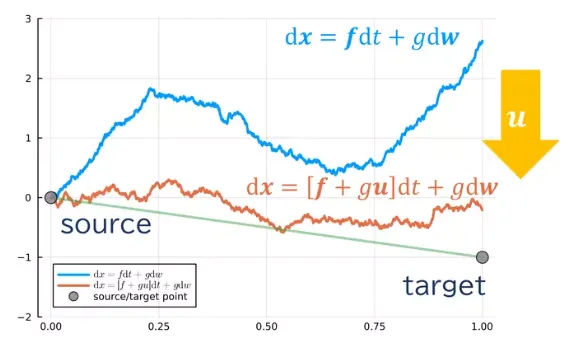
여기서는 T. Chen et al. (2021) (SB-FBSDE) 의 정식화를 소개
•
Dynamic SB는 등가 확률 최적 제어 문제로 변환할 수 있음이 알려져있습니다. [Caluya 19]
◦
여기서 dx=[f+gu]dt+g dw\mathrm{d} \boldsymbol{x}=[\boldsymbol{f}+g \boldsymbol{u}] \mathrm{d} t+g \mathrm{~d} \boldsymbol{w} 일때 상태 방정식
◦
참조 경로 측도 ℚ 보다 유도되는 확률장 (SDE: dx=fdt+g dw\mathrm{d} \boldsymbol{x}=\boldsymbol{f} \mathrm{d} t+g \mathrm{~d} \boldsymbol{w}） 을 떠도는 입자에 대하여 외력(𝒖)을 제어하여 초기치 x0\boldsymbol{x}_0에서 목표 xT\boldsymbol{x}_T 로 이끄는 문제
◦
최소의 작용 (∫∥u∥2 dt\int\|\boldsymbol{u}\|^2 \mathrm{~d} t） 으로 목적을 달성할 수 있을 때의 𝒖가 최적해
min⁡uE[∫0T12∥u(xt,t)∥2 dt] s.t. {dxt=[f(xt,t)+g(t)u(xt,t)]dt+g(t)dwtx0∼pdata xT∼pprior \begin{equation}\begin{aligned}& \min _{\boldsymbol{u}} \mathbb{E}\left[\int_0^T \frac{1}{2}\left\|\boldsymbol{u}\left(\boldsymbol{x}_t, t\right)\right\|^2 \mathrm{~d} t\right] \\& \text { s.t. }\left\{\begin{aligned}& \mathrm{d} \boldsymbol{x}_t=\left[\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)+g(t) \boldsymbol{u}\left(\boldsymbol{x}_t, t\right)\right] \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t \\& \boldsymbol{x}_0 \sim p_{\text {data }} \\& \boldsymbol{x}_T \sim p_{\text {prior }}\end{aligned}\right.\end{aligned}\end{equation}

SB 재정의: Schrodinger System

•
확률 최적 제어의 최적해 u∗\boldsymbol{u}^*는 함수 Ψ\Psi와 편미분방정식 (PDE) Ψ^\widehat{\Psi} 로 특정됩니다. [Caluya 19]
◦
이때 Ψ\Psi 는 Schrödinger potential, PDE Ψ^\widehat{\Psi} 는 Schrödinger system.
◦
각각 Kolmogorov의 Forward/Reverse Process에 해당하지만, 서로 다른 포텐셜을 사용함.
{ ∂Ψ∂t=−⟨∇Ψ,f⟩−12g2ΔΨ∂Ψ^∂t=−∇⋅[Ψ^f]+12g2ΔΨ^ s.t. {Ψ(⋅,0)Ψ^(⋅,0)=pdata Ψ(⋅,T)Ψ^(⋅,T)=pprior \begin{equation}\left\{\begin{array} { l } { \frac { \partial \Psi } { \partial t } = - \langle \nabla \Psi , \boldsymbol { f } \rangle - \frac { 1 } { 2 } g ^ { 2 } \Delta \Psi } \\{ \frac { \partial \widehat { \Psi } } { \partial t } = - \nabla \cdot [ \widehat { \Psi } \boldsymbol { f } ] + \frac { 1 } { 2 } g ^ { 2 } \Delta \widehat { \Psi } }\end{array} \text { s.t. } \left\{\begin{array}{l}\Psi(\cdot, 0) \widehat{\Psi}(\cdot, 0)=p_{\text {data }} \\\Psi(\cdot, T) \widehat{\Psi}(\cdot, T)=p_{\text {prior }}\end{array}\right.\right.\end{equation}
•
Schrödinger system의 해 Ψ\Psi, Ψ^\widehat{\Psi} 을 사용하면 ptp_t 와 u∗\boldsymbol{u}^*는 다음과 같습니다.
pt=Ψ(⋅,t)Ψ^(⋅,t)u∗=g(t)∇log⁡Ψ\begin{equation}\begin{gathered}p_t=\Psi(\cdot, t) \widehat{\Psi}(\cdot, t) \\\boldsymbol{u}^*=g(t) \nabla \log \Psi\end{gathered}\end{equation}
•
즉, 중간과정은 Ψ\Psi, Ψ^\widehat{\Psi} 와 xt\boldsymbol{x}_t를 따르는 밀도함수 ptp_t를 분해한 것으로 볼 수 있습니다.
•
구체적으로 Ψ\Psi, Ψ^\widehat{\Psi} 를 구하는 방법은 후술하겠습니다.

SB 재정의: Forward · Reverse SDE

•
상태 방정식의 제어 변수 u∗\boldsymbol{u}^*을 최적 포텐셜 Ψ\Psi, Ψ^\widehat{\Psi} 로 대체함으로써 SB의 해는 다음의Forward·Reverse SDE로 표현할 수 있습니다. [19]
◦
각 SDE는 reverse-time formula [12]에 의해 상호 변환 가능
Forward SDE: dxt=[f(xt,t)+g2(t)∇log⁡Ψ(xt,t)]dt+g(t)dwt,x0∼pdata Reverse SDE: dxt=[f(xt,t)−g2(t)∇log⁡Ψ^(xt,t)]dt+g(t)dwt,xT∼pprior \begin{align}\begin{equation} \begin{array}{ll} \text{Forward SDE: }& \mathrm{d} \boldsymbol{x}_t=\left[\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)+g^2(t) \nabla \log \Psi\left(\boldsymbol{x}_t, t\right)\right] \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t, & \boldsymbol{x}_0 \sim p_{\text {data }} \\ \text{Reverse SDE: }& \mathrm{d} \boldsymbol{x}_t=\left[\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)-g^2(t) \nabla \log \widehat{\Psi}\left(\boldsymbol{x}_t, t\right)\right] \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t, & \boldsymbol{x}_T \sim p_{\text {prior }} \end{array} \end{equation} \end{align}
•
즉, Schrödinger bridge 문제는 다음과 같이 바꿀 수 있습니다.
확률분포 pdata ,pprior p_{\text {data }}, p_{\text {prior }}와 참조측도 (확률장) Q:dx=fdt+g dw\mathbb{Q}: \mathrm{d} \boldsymbol{x}=\boldsymbol{f} \mathrm{d} t+g \mathrm{~d} \boldsymbol{w} 가 주어졌을 때, Schrödinger system을 만족시키는 함수 쌍 Ψ\Psi, Ψ^\widehat{\Psi} 을 구하는 문제.

SB 학습 및 생성과정

•
학습과정
1.
데이터 분포를 준비: pdata ,pprior p_{\text {data }}, p_{\text {prior }}
2.
기준 측도를 SDE로 설계: dx=fdt+g dw\mathrm{d} \boldsymbol{x}=\boldsymbol{f} \mathrm{d} t+g \mathrm{~d} \boldsymbol{w}
3.
Schrödinger system을 충족시키기 위해 매개변수화 된 모델 훈련 (Ψ\Psi, Ψ^\widehat{\Psi} 중간 학습)
•
생성과정
1.
초기 데이터 x를 pprior p_{\text {prior }}에서 샘플
2.
학습된 모델을 사용하여 초기조건 x 하에서 Reverse SDE를 품: dx=[f−g2∇log⁡Ψ^]dt+g dw\mathrm{d} \boldsymbol{x}=\left[\boldsymbol{f}-g^2 \nabla \log \widehat{\Psi}\right] \mathrm{d} t+g \mathrm{~d} \boldsymbol{w}

SGM과의 관계

•
SB는 확산모델의 확장이라고 볼 수 있습니다.
•
확산 모델의 Forward Reverse SDE는 Ψ≡1,p(xT∣x0)=N(0,I)\Psi \equiv 1, p\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)=N(\mathbf{0}, \boldsymbol{I}) 의 제약은 둔 SB와 같습니다.
•
이 때, g2∇log⁡Ψ≡0,Ψ^=ΨΨ^=pg^2 \nabla \log \Psi \equiv 0, \widehat{\Psi}=\Psi \widehat{\Psi}=p 가 성립합니다.
•
더 엄밀히 말하면, 사전 분포의 제약 조건을 푸는 대신 전진 과정도 학습 파라미터화한 확산 모델이 Schrödinger bridge입니다.

결론

•
Schrödinger Bridge (SB)는 사전 분포의 제약을 완화 한 확산 모델입니다.
•
SB는 Dynamic Optimal Transport 문제로 간주 될 수 있습니다.
•
T. Chen et al. (2021)에 따르면 Forward 및 Reverse Process SDE의 동시 최적화로 볼 수 있습니다.

더 알아볼 내용

1.
기준 경로 측도 Q\mathbb{Q}의 설계 방법
•
확률 최적 제어 문제의 확률 필드 (SDE) dxt=f(xt,t)dt+g(t)dwt\mathrm{d} \boldsymbol{x}_t=\boldsymbol{f}\left(\boldsymbol{x}_t, t\right) \mathrm{d} t+g(t) \mathrm{d} \boldsymbol{w}_t
•
드리프트 계수 f(xt,t)\boldsymbol{f}\left(\boldsymbol{x}_t, t\right)와 확산 계수 g(t)g\left(t\right)는 어떻게 설계해야 할까?
2.
SB 모델 훈련 알고리즘
•
Schrödinger potential Ψ\Psi, Ψ^\widehat{\Psi}의 최적 해를 구하는 방법
•
기계 학습 프레임 워크에 가져올 때, 어떻게 매개 변수화하는 것이 바람직할까?
•
Iterative Proportional Fitting (IPF) [Bortoli 21, Vargas 21]
◦
Optimal Transport Sinkhorn-Knopp [Curturi 13] 알고리즘의 확장
•
Forward-backward SDE (SB-FBSDE)
•
Iterative Markov Fitting (IMF)
•
Computer Vision 응용
◦
Image-to-image Schrödinger Bridge (I2SB)
•
관련 알고리즘
◦
Conditional Flow Matching (CFM) (Tong 23, Kerrigan 24)
◦
Simulation-Free Score and Flow Matching ([SF]2M)