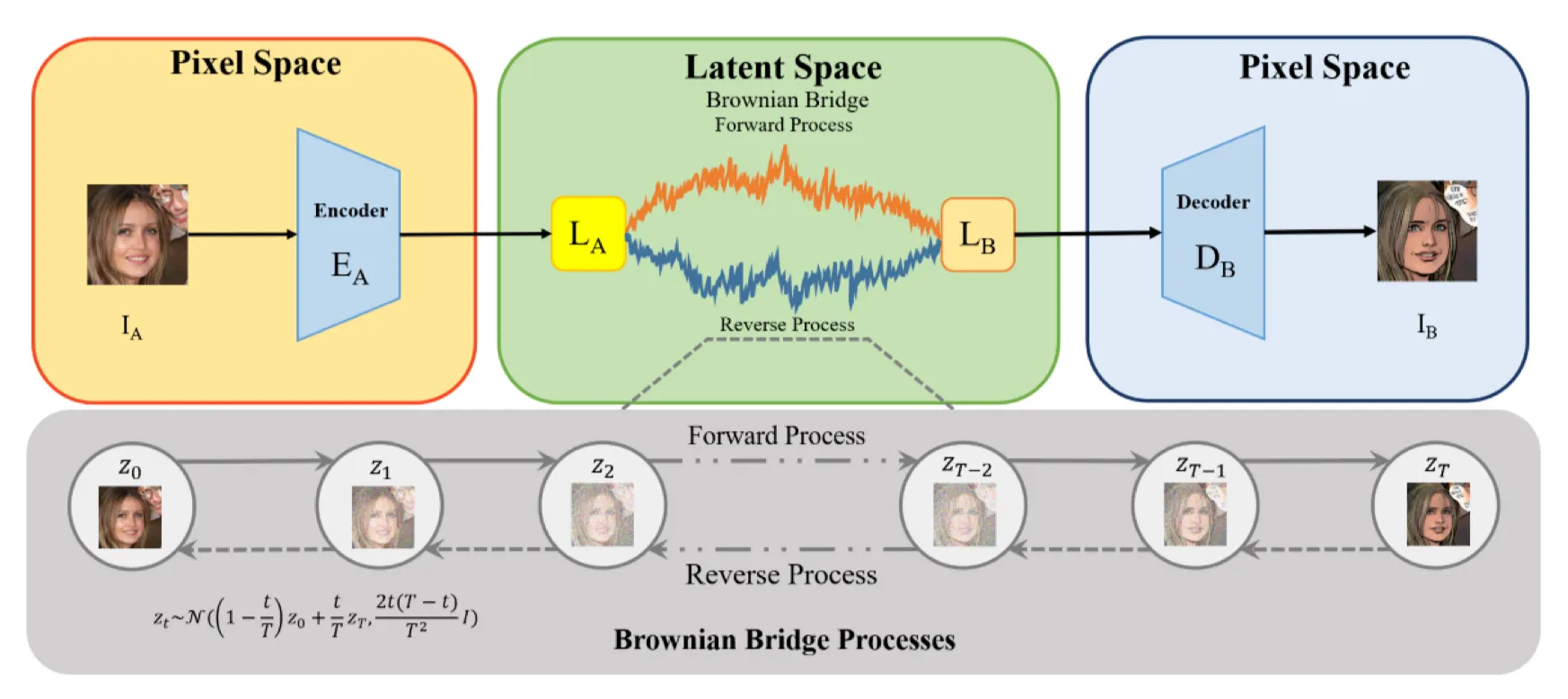
BBDM: Image-to-image Translation with Brownian Bridge Diffusion Models
Intro & Overview
Prelinamaries: DDPMs
DDPM에 대한 간략한 요약을 하며 시작하겠습니다.
DDPM의 Forward Process와 Reverse process 그리고 Training Objective는 다음과 같이 정의됩니다.
DDPM: Forward Process
•
Forward Process는 Data에 노이즈를 점진적으로 더해가는 과정입니다.
•
Data 에서 시작합니다.
•
최종 Latent variable 이며 인 isotropic Gaussian distribution입니다.
•
에서 로 변환하는 과정은 Markov chain으로 정의됩니다.
•
는 아주 작은 상수.
DDPM: Reverse Process.
•
Reverse Process는 Latent variable 로부터 데이터 를 추론하는 과정입니다.
•
이는 다음과 같은 Markov chain으로 정의됩니다.
DDPM: Training Objective
•
DDPM은 Evidence Lower Bound (ELBO)를 이용하여 최적화됩니다.
•
: 의 가우시안 노이즈. .
•
: denoising model.
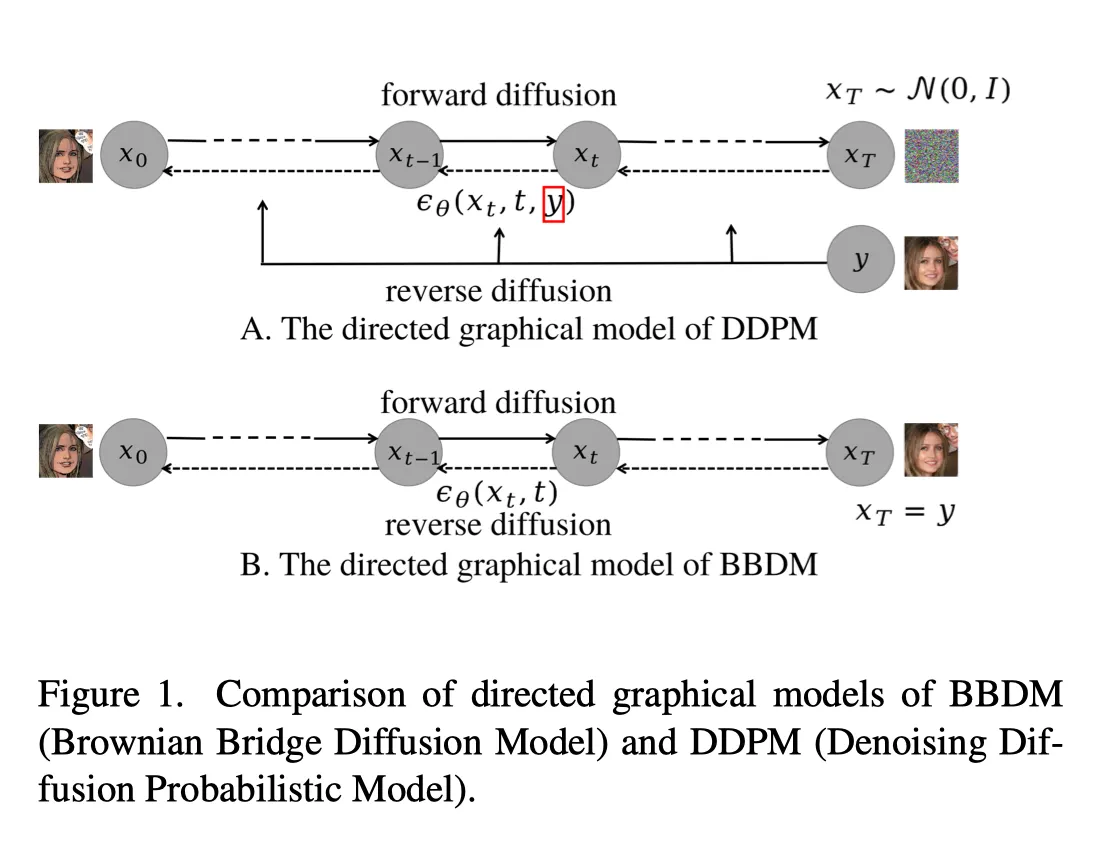
Conditional Diffusion.
•
대부분의 conditional diffusion model들은 condition을 Objective에 직접적으로 주입합니다.
•
하지만, 가 이 Objective에 명확히 정의되지 않으므로 생성 결과가 condition에 부합하는지 단언할 수 없습니다.
Prelinamaries: Brownian Bridge
•
Brownian bridge 모델은 continous-time stochastic 모델입니다.
•
이때 condtion은 start point와 ending point에 의해 정해집니다.
•
즉, 노이즈에서 데이터로 변했던 기존 모델과 달리 데이터에서 데이터로 변하게 됩니다.
•
Brownian Bridge Process는 다음과 같이 정의됩니다.
•
식은 간단합니다. T에 대한 t의 비율로 와 를 Linear하게 섞어줍니다.
•
노이즈는 양 극단에서 최소가 되고, 중간에서 최대가 됩니다.
Methodology
Brownian Bridge Diffusin Model 위 Brownian Bridge Process를 적용하면 다음과 같습니다.
•
이때, 식 (4)에 따라 variance는 인데 일때 가 됩니다.
•
이는 T가 매우 커짐에 따라 더욱 큰 값이 됩니다.
•
따라서 variance를 보존 (Preserving) 할 수 있도록 다음과 같이 디자인합니다.
•
이때 s는 scale factor 로써 sampling diversity를 컨트롤합니다. ( by default)
Forward Process:
•
위 식 (5) 를 통해 을 구하여 대입해주면 다음과 같습니다.
Reverse Process 에서 출발해 에 도달하는 reverse process는 다음과 같습니다.
•
이때, : predicted mean value of noise
: variance of noise at each step.
Objective ELBO를 사용합니다.
•
첫 항은 constant가 되어 KL Divergence는 0이 됩니다.
•
두번째 항은 식 (5)와 (7) 그리고 Bayes’ theorem, Markov chain property를 이용해 다음과 같이 나타냅니다.
•
이때, 가 unknown이므로 reparametrization trick을 사용합니다.
•
여기서 가 아닌 노이즈 를 예측하도록 하면 다음과 같은 Linear combindation이 됩니다.
•
따라서, ELBO (식 10)은 다음과 같습니다.
수식으로 보나 코드로 보나 사실 별거 없습니다.
샘플에 노이즈를 더한 후 (target) L2 로스를 계산하면 끝입니다.
Sampling
사실 큰 의미는 없습니다. 샘플러 step = 200 에 대해 DDPM 샘플링을 하겠다는 뜻입니다.
Experimental Results
Conclusion
•
굉장히 간단한 논문이지만, 기존의 Bridge Model과 다르게 간단한 수식만으로 DDPM의 VP 프레임워크로 명료화했다는 점에서 다른 Application으로 발판을 마련했다고 볼 수 있습니다.
•
최근의 많은 Architectural 한 논문들은 거진 DDPM을 기반으로 하고 있는 것 처럼요.
•
Bridge Diffusion Model은 Condition의 개입 없이도 Image-to-image task를 수행할 수 있다는 점에서 모델 복잡도, 훈련 시간, 차원 복잡도에서 큰 이득이 있습니다. (논문에는 언급되지 않았지만 이러한 이점이 Bridge Model의 가장 큰 장점이라고 생각합니다.)
•
이를 베이스로 한 저의 논문이 곧 publish 될 예정이니 기대해주시면 감사드리겠습니다.