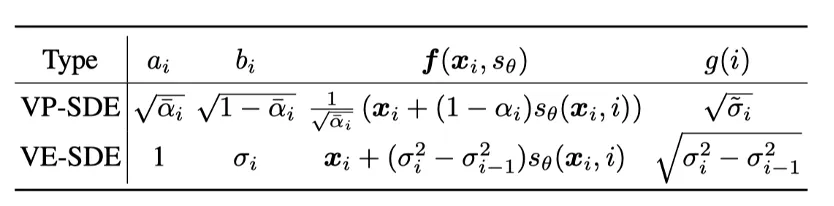//
Search
⌛

Diffusion Theory Summary

Diffusion Series
Diffusion Theory Summary
Image-to-image Translation
EGSDE: Unpaired I2I Translation via Energy-Guided SDEs.
SDDM: Score-Decomposed Diffusion Models on Manifolds for Unpaired I2I Translation
On Writing.

Score-based Diffusion Models (SBDMs)

•
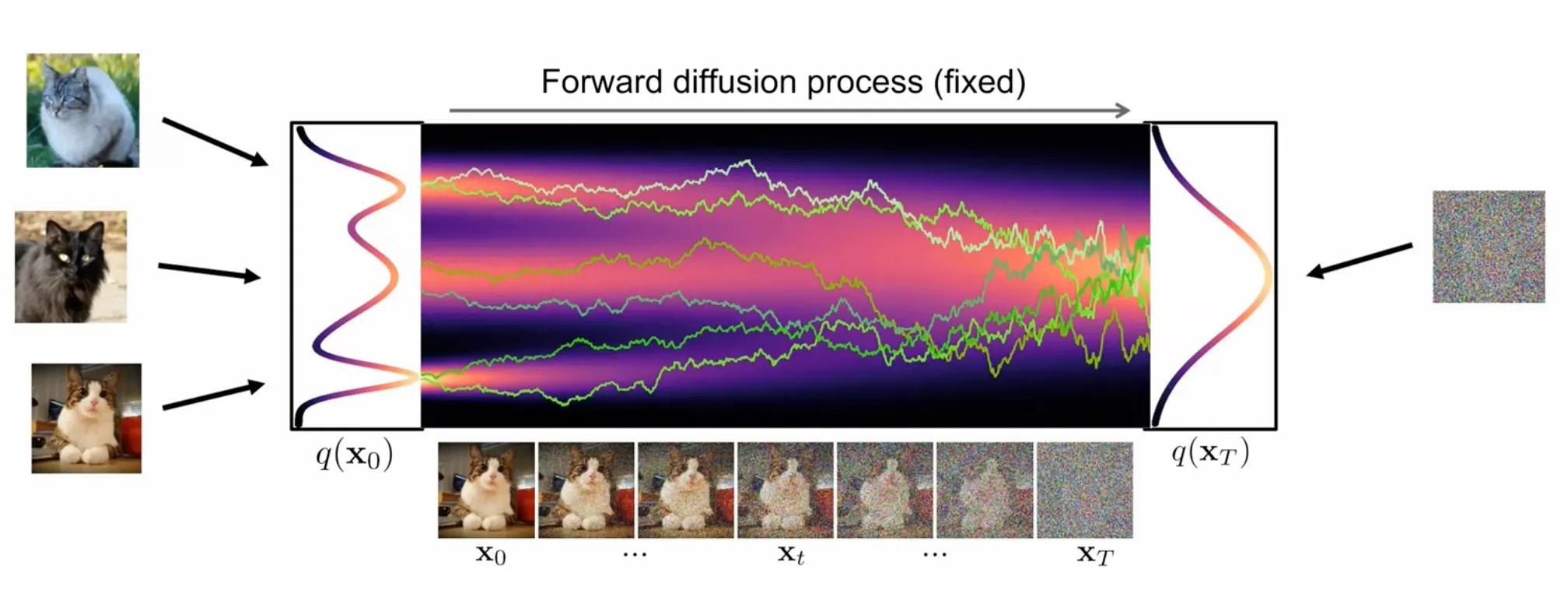
SBDMs first progressively perturb the training data via a forward diffusion process.
•
And then learn to reverse this process to form a generative model of the unknown data distribution.

Forward Process

•
q(x0)q(\mathbf{x}_0): training set with i.i.d. samples on Rd\mathbb{R}^d.
•
q(xt)q(\mathbf{x}_t): Intermediate distribution at time t.
•
{xt}t∈[0,T]\{\mathbf{x}_t\}_{t\in[0,T]}: Forward diffusion process following SDEs.
dx=f(x,t)dt⏟Drift Term(vector)+g(t)dw⏟diffusion term(scalar)\text{d}\mathbf{x}= \underbrace{ \mathbf{f}(\mathbf{x},t)\text{d}t }_{\substack{ \text{Drift Term}\\ \text{(vector)} }} + \underbrace{ g(t)\text{d}\mathbf{w} }_{\substack{ \text{diffusion term} \\ \text{(scalar)} }}
f(⋅,t):Rd→Rd\mathbf{f}(\cdot,t): \mathbb{R}^d\rightarrow \mathbb{R}^d: drift coefficient.
g(t)∈R\mathbf{g}(t)\in \mathbb{R}: diffusion coeffisient.
dt\text{d}t: infinitesimal positive timestep.
dw∼N(0,tId)\text{d}\mathbf{w}\sim\mathcal{N}(0,t\mathbf{I}_d): standard Wiener process.
•
Denote qt∣0(xt∣x0)q_{t|0}(\mathbf{x}_t|\mathbf{x}_0): transition kernel from timestep 0 to t, which decided by f\mathbf{f} and g\mathbf{g}.
•
f(x,t)\mathbf{f}(\mathbf{x},t) is usually an affine transformation w.r.t. x\mathbf{x} so that the qt∣0(xt∣x0)q_{t|0}(\mathbf{x}_t|\mathbf{x}_0) is a linear Gaussian distribution and xt\mathbf{x}_t can be sampled in one step. [Zhao et.al. 2021]
•
VP-SDE (Variance-preserving SDE)
dx=−12β(t)xdt+β(t)dw\text{d}\mathbf{x}= - \frac{1}{2}\beta(t) \mathbf{x}\text{d}t + \sqrt{\beta(t)} \text{d}\mathbf{w}

Reverse Process

•
Reverse SDE by Anderson’s theorem: [Song et al. (2021)]
dx=[ f(x,t)−g2(t)∇xlog⁡pt(x)⏟score function ]dt+g(t)dwˉ\text{d}\mathbf{x}= [\ \mathbf{f}(\mathbf{x},t) - \mathbf{g}^2(t) \underbrace{ \nabla_\mathbf{x}\log p_t(\mathbf{x}) }_{\substack{ \text{score function} }} \ ]\text{d}t + g(t)\text{d}\bar{\mathbf{w}}
•
dwˉ\text{d}\bar{\mathbf{w}}: standard Wiener process backward in time.
•
score-based model sθ(x,t)≐∇xlog⁡qt(x)\mathbf{s}_\theta (\mathbf{x},t) \doteq \nabla_{\mathbf{x}}\log q_t(\mathbf{x}) (approximate)
dx=[ f(x,t)−g2(t)sθ(x,t)⏟score model ]dt+g(t)dwˉ\text{d}\mathbf{x}= [\ \mathbf{f}(\mathbf{x},t) - \mathbf{g}^2(t) \underbrace{\mathbf{s}_\theta(\mathbf{x},t) }_{\substack{ \text{score model} }} \ ]\text{d}t + g(t)\text{d}\bar{\mathbf{w}}

General Forms

z∼N(0,I)\mathbf{z}\sim\mathcal N(0,\mathbf{I}): Gaussian Noise.
•
Forward Process: xi=aix0+biz\mathbf{x}_i=a_i\mathbf{x}_0+b_i \mathbf{z}
•
Backward Process: xi−1=f(x,t)dt+g(xi)z\mathbf{x}_{i-1}=\mathbf{f}(\mathbf{x},t)\text{d}t+g(\mathbf{x}_i)\mathbf{z}
•
Choice of f, g, a, b:
VP-SDE (DDPMs)
•
linear noise schedule: {βt}t=0T∈(0,1)\{\beta_t\}^T_{t=0}\in(0,1)
⇒ xi=αtˉx0+1−αtˉϵ\mathbf{x}_i = \sqrt{\bar{\alpha_t}}\mathbf{x}_0 + \sqrt{1-\bar{\alpha_t}}\mathcal{\epsilon}
VE-SDE (SGBMs)
•
Geometrical noise schedule: σi=σ0(σN/σ0)i−1N−1\sigma_i=\sigma_0(\sigma_N / \sigma_0)^{\frac{i-1}{N-1}}
⇒ xi=x0+σiz\mathbf{x}_i=\mathbf{x}_0+\sigma_i\mathbf{z}

Controllable Generation

•
add guidance function ϵ(x,t)\red{\epsilon(\mathbf{x},t)} to the score function:
dx=[ f(x,t)−g2(t)(sθ(x,t)⏟score model+∇xϵ(x,t)⏟guidance ]dt+g(t)dwˉ\text{d}\mathbf{x}= [\ \mathbf{f}(\mathbf{x},t) - \mathbf{g}^2(t)( \underbrace{\mathbf{s}_\theta(\mathbf{x},t) }_{\substack{ \text{score model} }} + \underbrace{ \red{ \nabla_{\mathbf{x}} \epsilon(\mathbf{x},t)} }_{\substack{ \text{guidance} }} \ ]\text{d}t + g(t)\text{d}\bar{\mathbf{w}}

Classifier Guidance

dx=[ fˉ(x,t)−gˉ2(t)∇xlog⁡pt(x∣y)]dt+gˉ(t)dwˉ=[ fˉ(x,t)−gˉ2(t)[∇xlog⁡pt(x)⏟uncond. model−∇xlog⁡pt(y∣x)⏟classifier]]dt+gˉ(t)dwˉ\begin{align} \text{d}\mathbf{x} &= \left[\ \bar{\mathbf{f}}(\mathbf{x},t) - \bar{g}^2(t) \red{ \nabla_{\mathbf{x}} \log p_t(\mathbf{x|y})} \right]\text{d}t + \bar g(t)\text{d}\bar{\mathbf{w}} \\ &= \left[\ \bar{\mathbf{f}}(\mathbf{x},t) - \bar{g}^2(t) [ \underbrace{ \red{\nabla_{\mathbf{x}} \log p_t(\mathbf{x})}} _{\text{uncond. model}} - \underbrace{ \red{\nabla_{\mathbf{x}} \log p_t(\mathbf{y|x})} }_{\substack{ \text{classifier} }} ] \right] \text{d}t + \bar g(t)\text{d}\bar{\mathbf{w}} \end{align}

Unpaired I2I + SBDMs

•
Formulation Transfer Source image in source domain Y∈Rd\mathcal{Y}\in \mathbb{R}^d to target domain X∈Rd\mathcal{X}\in\mathbb{R}^d.
•
Goal Designing a distribution p(x0∣y0)p(\mathbf{x}_0|\mathbf{y}_0) on target domain X\mathcal{X} conditioned on an image y0∈Y\mathbf{y}_0 \in \mathcal{Y} to transfer.

ILVR (Choi. et al., 2021)

xt′=xt−Φ(xt)+Φ(yt),yt∼qt∣0(yt∣y0)\mathbf{x}'_t=\mathbf{x}_t-\mathbf{\Phi}(\mathbf{x}_t)+\mathbf{\Phi}(\mathbf{y}_t), \quad \mathbf{y}_t\sim q_{t|0}(\mathbf{y}_t|\mathbf{y}_0)
•
refine xt\mathbf{x}_t after each denoising step with a LPF Φ\mathbf{\Phi}.

EGSDE (Zhao et al., 2022)

dx=[ f(x,t)−g2(t)(sθ(x,t)+∇xϵ(x,y0,t)⏟guidance ]dt+g(t)dwˉ\text{d}\mathbf{x}= [\ \mathbf{f}(\mathbf{x},t) - \mathbf{g}^2(t)( \mathbf{s}_\theta(\mathbf{x},t) + \underbrace{ \red{ \nabla_{\mathbf{x}} \epsilon(\mathbf{x},\mathbf{y}_0,t)} }_{\substack{ \text{guidance} }} \ ]\text{d}t + g(t)\text{d}\bar{\mathbf{w}}
•
design two energey-based guidance functions and follow cond. generation Song 2021.

DDPM

Forward Process

q(xt∣xt−1)=N(1−βtxt−1,βtI)\begin{align} q(x_t|x_{t-1})=\mathcal{N}(\sqrt{1-\beta_t}x_{t-1},\beta_t I) \end{align}
q(xt∣x0)=N(xt;αtˉx0,(1−αˉt)I)\begin{align} q(x_t|x_0)&=\mathcal{N} (x_t;\sqrt{\bar{\alpha_t}}x_0,(1-\bar{\alpha}_t)I) \end{align}
where αt=1−βt\alpha_t = 1-\beta_t and αˉt=∏i=1tαt\bar{\alpha}_t=\prod_{i=1}^{t}{\alpha_t}.
•
for sampling:
xt=αˉtx0+(1−αˉt)ϵx_t=\sqrt {\bar\alpha_t } x_0+\sqrt{(1-\bar\alpha_t)}\epsilon
q(xt)⏟Diffused datadist.=∫q(x0,xt)⏟Joint dist.dx0=∫q(x0)⏟Input datadist.q(xt∣x0)⏟Diffusionkerneldx0\begin{align} \underbrace{q(x_t)}_{\substack{\text{Diffused data} \\ \text{dist.}}} =\int{\underbrace{q(x_0,x_t)}_{\text{Joint dist.}}}dx_0=\int{\underbrace{q(x_0)}_{\substack{\text{Input data} \\ \text{dist.}}}\underbrace{q(x_t|x_0)}_{\substack{\text{Diffusion} \\ \text{kernel}}}dx_0} \end{align}
More Detailed Explain.

Reverse Process

pθ(xt−1∣xt)=N(μθ(xt,t),Σθ(xt,t))=N(μθ(xt,t)⏟Trainable network,σt2)pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt)\begin{align} p_\theta (x_{t-1} | x_t)&=\mathcal N \left(\mu_\theta (x_t,t), \Sigma_\theta(x_t,t)\right)\\ &=\mathcal N ( \underbrace{\red{\mu_\theta (x_t,t)}}_{\substack{\text{Trainable }\\ \text{network}}} , \sigma_t^2 )\\ p_\theta (x_{0:T})&= p(x_T)\prod^T_{t=1}p_\theta(x_{t-1}|x_t) \end{align}

Training

option #1 Predict x0x_0 directly as μθ(xt,t)\mu_\theta(x_t,t).
option #2 Predict the original t=0t=0 sample x0x_0, where
μθ~=αˉt−1βt1−αˉtx0+αt1−αˉt−11−αˉtxt\tilde{\mu_\theta}=\sqrt{\bar{\alpha}_{t-1}}\frac{\beta_t}{1-\bar{\alpha}_t}x_0+\sqrt{\alpha_t}\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\blue{x_t}
option #3 Predict the normal noise sample ϵ\epsilon which has been added to the x0x_0.
x0=1αˉt(xt−1−αˉtϵ)x_0=\frac{1}{\sqrt{\bar\alpha_t}}(\blue{x_t}-\sqrt{1-\bar\alpha_t}\red{\epsilon})
μ~θ=αˉt−1⋅βt1−αˉt(1−1αˉt(xt−1−αˉtϵ))+αt⋅1−αˉt−11−αˉtxt\tilde\mu_\theta=\sqrt{\bar{\alpha}_{t-1}}\cdot\frac{\beta_t}{1-\bar{\alpha}_t}\left(1-\frac{1}{\sqrt{\bar\alpha_t}}(\blue{x_t}-\sqrt{1-\bar\alpha_t}\red{\epsilon})\right)+\sqrt\alpha_t\cdot\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\blue{x_t}
and hence
μ~θ=1αt(xt−βt1−αˉtϵ)\tilde\mu_\theta=\frac{1}{\sqrt\alpha_t}(\blue{x_t}-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\red{\epsilon})

Loss: VAE to DDPM

Loss

Algorithm

1.
Forward Process: sample xt∼q(xt∣x0)x_t\sim q(x_t|x_0) for t:[1,T]t: [1,T].
a.
sample t∼U(1,T)t \sim \mathcal{U}(1,T).
b.
sample ϵ∼N(0,1)\epsilon\sim \mathcal{N}(0,1) . (가우시안 샘플링)
c.
compute xt=αˉtx0+1−αˉtϵx_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon. (Forward)
2.
Compute noise: ϵ^t=pθ(xt,t)\hat{\epsilon}_t=p_\theta(x_t,t) using model with parameter θ\theta.
3.
Minimize error: ϵ~t\tilde\epsilon_t and ϵt\epsilon_t by optimizing parameter θ\theta.

Sampling

1.
Sample noise xT∼N(0,1)x_T \sim\mathcal N (0,1). (가우시안 샘플링)
2.
Predict the noise in the sample: ϵ~=pθ(xt,t)\tilde{\epsilon}=p_\theta(x_t,t) and approximate the mean of the process at t−1t-1.
μθ~=1αt(xt−βt1−αtˉϵ~)\tilde{\mu_\theta}=\frac{1}{\sqrt{\alpha_t}}(\blue{x_t}-\frac{\beta_t}{\sqrt{1-\bar{\alpha_t}}}{\red{\tilde\epsilon}})
3.
Next sample at t=1t=1 is sampled from Gaussian distribution as:
xt−1∼N(μ~θ,σt2I)x_{t-1}\sim\mathcal N (\tilde \mu_\theta,\sigma^2_t I)
...until x0x_0 is reached, in which case only the mean μ~θ\tilde\mu_\theta is extracted as output.
•
better sample quality at fewer steps.
•
Allows for deterministic matching between the starting noise xTx_T and the generated sample x0x_0.
•
Perform worse that DDPM for large numbers of steps ( e.g. 1000).

Noise Schedule

Visualization

•
βt\beta_t: Low Frequency 혹은 High Frequency를 만들 것인지 네트워크에게 알려주는 역할

Summary

DDIM: Sampling Faster. Non-Markovian process.

•
DDPM (Markovian) → DDIM (Non-Markovian).
•
다 같고, 샘플링만 다르다.
Details
From DDPM equation (1) at t−1t-1,
q(xt−1∣x0)=N(αˉt−1x0,(1−αˉt−1)I)\begin{equation} q(x_{t-1}|x_0)=\mathcal{N}(\sqrt{\bar\alpha_{t-1}}x_0,(1-\bar{\alpha}_{t-1})I) \end{equation}
which yields,
xt−1←αˉt−1x0+1−αˉt−1ϵt−1\begin{align} x_{t-1}&\leftarrow \sqrt{\bar\alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t-1}}\epsilon_{t-1} \end{align}
based on specific ϵt\epsilon_t measured at the previous step tt,
xt−1←αˉt−1x0+1−αˉt−1−σt2ϵt+σtϵ\begin{align} x_{t-1}&\leftarrow \sqrt{\bar\alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t-1}-\sigma^2_t}\epsilon_t+\sigma_t\epsilon \end{align}
if ϵ\epsilon=0, deterministic. (noise:image=1:1 matching)
Generally, σt\sigma_t is set to:
σt2=β~t=1−αˉt−11−αˉtβt\sigma^2_t=\tilde\beta_t=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t
new parameter η\eta to comtrol the magnitude of the stochastic component:
σt2=ηβ~t\sigma^2_t=\eta\tilde\beta_t
•
η=0\eta=0: appears to be particularly beneficial when fewer steps of the reverse process are applied and that specific type of process is known as DDIM.
•
η=1\eta=1: DDPM.
So, how can the reverse chain be navigated in the reverse direction?
•
First, a sequence of fewer steps SS is defined as a subset {τ1,τ2,...,τS}\{\tau_1, \tau_2, ..., \tau_S\} of the original temporal steps of the forward process. Sampling is then based on (8).

DDIM: Sampling

1.
predict x0x_0.
2.
Compute the direction towards current xtx_t.
3.
(if not DDIM) inject noise for stochastic functionality.

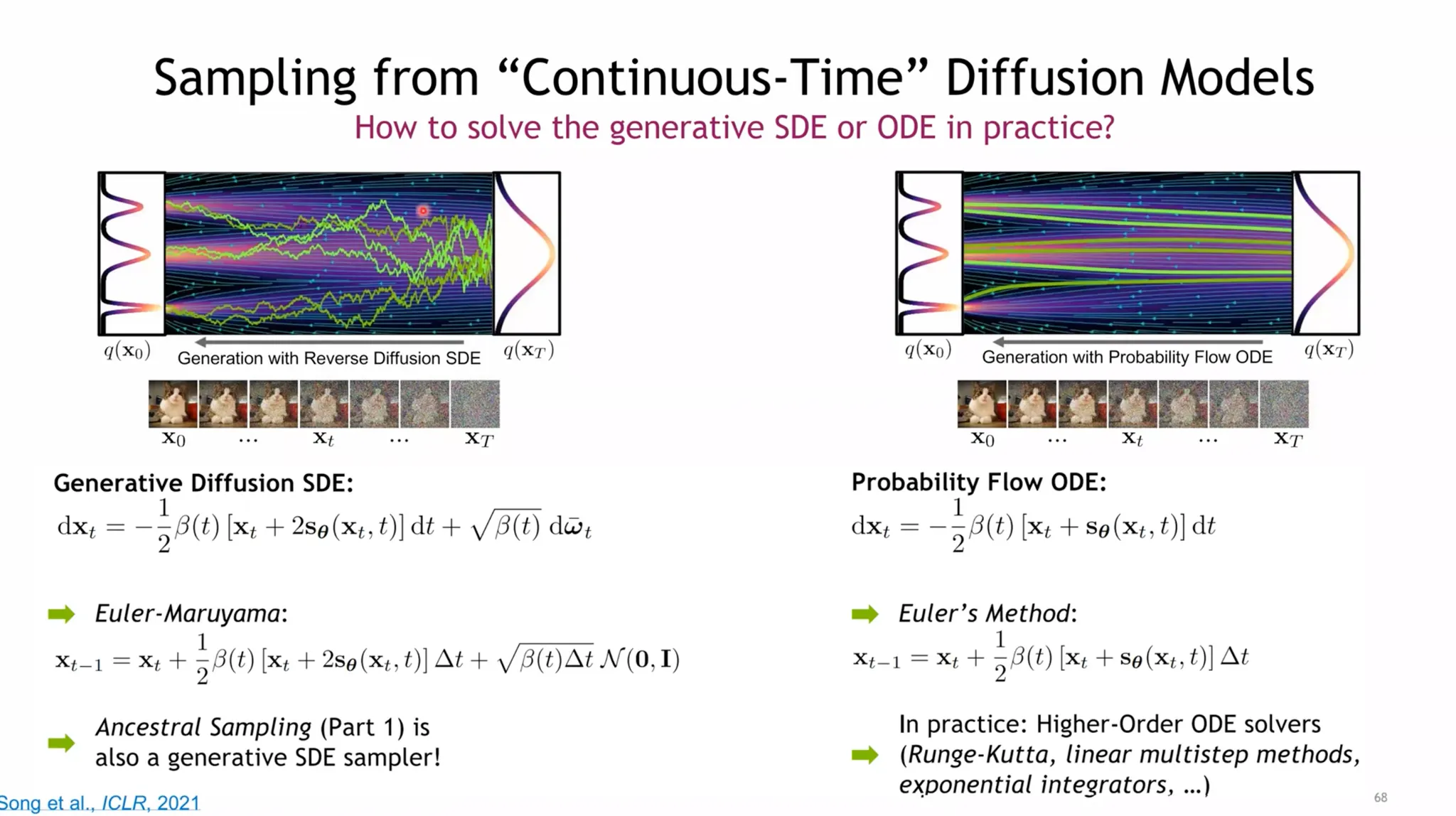
SBDMs

Visualization
q(xt∣xt−1)=N(xt,1−βtxt−1βt,I)→xt=1−βtxt−1+βt⋅N(0,I)(βt:=β(t)Δt)=1−β(t)Δtxt−1+β(t)Δt⋅N(0,I)≈xt−1−β(t)Δt2xt−1+β(t)Δt⋅N(0,I)\begin{align*} q(x_t|x_{t-1})&=\mathcal N (x_t,\sqrt{1-\beta_t}x_{t-1}\beta_t, I) \\ \rightarrow x_t&=\sqrt{1-\beta_t}x_{t-1}+\sqrt{\beta_t}\cdot \mathcal N (0,I) \\ (\beta_t:=\beta(t)\Delta t) &=\sqrt{1-\beta(t)\Delta t}x_{t-1} +\sqrt{\beta(t)\Delta t}\cdot\mathcal N (0,I) \\ &\approx x_{t-1} -\frac{\beta(t)\Delta t}{2}x_{t-1} +\sqrt{\beta(t)\Delta t}\mathcal \cdot N (0,I) \end{align*}
미분방정식처럼 생겼지? Solve with SDE.
Forward SDE:
dxt=−12β(t)xtdt⏟drift term+β(t)dωt⏟diffusion termdxt=f(t)xtdt+g(t)dωt\begin{align} \text{d}x_t &=\underbrace{-\frac{1}{2}\beta(t)x_t\text{d}t}_{\text{drift term}} +\underbrace{\sqrt{\beta(t)}\text{d}\omega_t}_{\text{diffusion term}} \\ \text{d}x_t&=f(t)x_t\text{d}t+g(t)\text{d}\omega_t \end{align}
Reverse SDE (Anderson 1982)
dxt=[−12β(t)xtdt−β(t)∇xtlog⁡qt(xt)⏟score function]⏞drift termdt+β(t)dωt⏞diffusion term\begin{equation} \text{d}x_t=\overbrace{\Big[ -\frac{1}{2}\beta(t)x_t\text{d}t -\beta(t) \underbrace{ \red{\nabla_{x_t} \log q_t(x_t)}} _{\text{score function}} \Big]} ^{\text{drift term}}\text{d}t +\overbrace{ \sqrt{\beta(t)}\text{d}\omega_t} ^{\text{diffusion term}} \end{equation}
•
To Solve Reverse SDE, How to get score function?
option #1 Naive way: NN으로 score func. 학습.
min⁡θE⁡t∼U(0,T)⏟diffusion time tExt∼qt(xt)⏟diffused data xt∥s⁡θ(xt,t)⏟neuralnetwork−∇xtlog⁡qt(xt)⏟Score of diffused data(marginal)∥22\min_\theta \underbrace{ \operatorname{\mathbb E}_{t\sim \mathcal U(0,T)}} _{\substack{ \text{diffusion }\\ {\text{time }t}}} \underbrace{ \mathbb E_{x_t\sim \mathcal q_t(x_t)}} _{\substack{ \text{diffused }\\ {\text{data }x_t}}} \lVert \underbrace{ \operatorname{s}_\theta(x_t,t)} _{\substack{ \text{neural}\\ \text{network}}} - \underbrace{ \nabla_{x_t}\log q_t (x_t) } _{\substack{ \text{Score of diffused data}\\ \text{(marginal)}}} \rVert^2_2
⇒ But score of marginal diffused density qt(xt)q_t(x_t) is not tractable!
중간 timestep을 알 수 없어서 학습이 안됨.
option #2 Given x0x_0.
•
Denoised score matching:
min⁡θEt∼U(0,T)⏟diffusion time tEx0∼q0(x0)⏟data sample x0Ext∼qt(xt)⏟diffused data xt∥s⁡θ(xt,t)⏟neuralnetwork−∇xtlog⁡qt(xt∣x0)⏟Score ofdiffused data sample∥22\min_\theta \underbrace{ \mathbb E _{t\sim \mathcal U(0,T)}} _{\substack{ \text{diffusion }\\ {\text{time }t}}} \underbrace{ \mathbb E _{x_0\sim \mathcal q_0(x_0)}} _{\substack{ \text{data }\\ {\text{sample }x_0}}} \underbrace{ \mathbb E _{x_t\sim \mathcal q_t(x_t)}} _{\substack{ \text{diffused }\\ {\text{data }x_t}}} \lVert \underbrace{ \operatorname{s}_\theta(x_t,t)} _{\substack{ \text{neural}\\ \text{network}}} - \underbrace{ \nabla_{x_t}\log q_t (x_t|x_0) } _{\substack{ \text{Score of}\\ \text{diffused data sample}}} \rVert^2_2
⇒ After expectation,
s⁡θ(xt,t)≈∇xtlog⁡qt(xt)\operatorname{s}_\theta(x_t,t) \approx \nabla_{x_t} \log q_t(x_t)
Details
•
Consider reverse generative diffusion SDE:
dxt=−12β(t)[xt+2∇xtlog⁡qt(xt)]dt+β(t)dωˉt\text{d}x_t =-\frac{1}{2}\beta(t) \Big[ x_t + 2\nabla_{x_t}\log q_t(x_t) \Big]\text{d}t + \sqrt{\beta(t)} \text{d} \bar{\omega}_t
•
In distribution equivalent to “Probability Flow ODE”:
•
initializing qT(xT)≈(xT;0,I))q^T(x^T)\approx(x_T;0,I))
dxt=−12β(t)[xt+2∇xtlog⁡qt(xt)]dt\text{d}x_t =-\frac{1}{2}\beta(t) \Big[ x_t + 2\nabla_{x_t}\log q_t(x_t) \Big]\text{d}t

Conditional Generation

dx=[f(x,t)−g2(t)∇xlog⁡pt(x∣y)]dt+g(t)dw=[f(x,t)−g2(t)[∇xlog⁡pt(x)⏟UnconditionalScore Function(Pretrained)−∇xlog⁡pt(y∣x)⏟Score Function과별개로 학습]]dt+g(t)dw\begin{align} \text{d}x &=\Big[ f(x,t) -g^2(t) \textcolor{coral}{{\nabla_x\log p_t(x|y)}} \Big]\text{d}t +g(t)\text{d}w \\ &=\Big[ f(x,t) -g^2(t)\big[ \underbrace{ \textcolor{burlywood}{\nabla_x\log p_t(x)}} _{\substack{ \text{Unconditional}\\ \text{Score Function}\\ \text{(Pretrained)} }} - \underbrace{ \textcolor{burlywood}{ \nabla_x\log p_t(y|x) }}_{\substack{ \text{Score Function과}\\ \text{별개로 학습} } }\big] \Big]\text{d}t +g(t)\text{d}w \end{align}