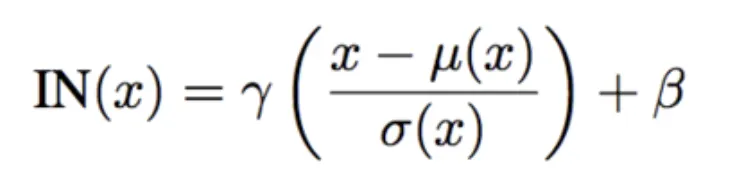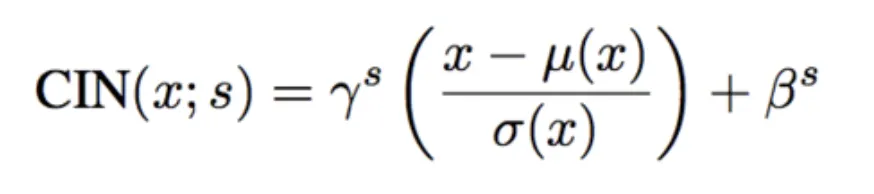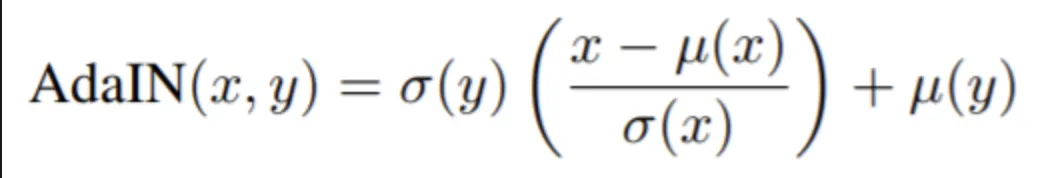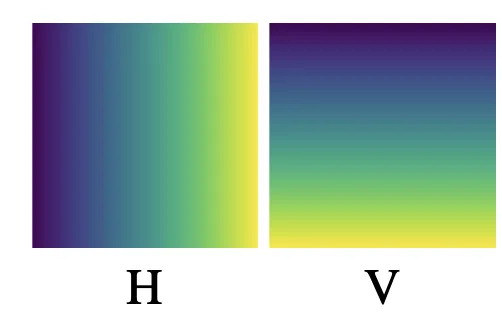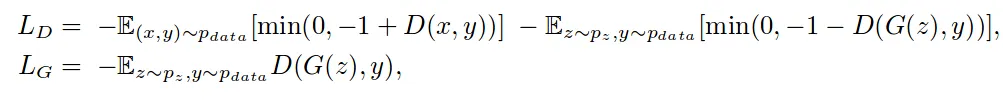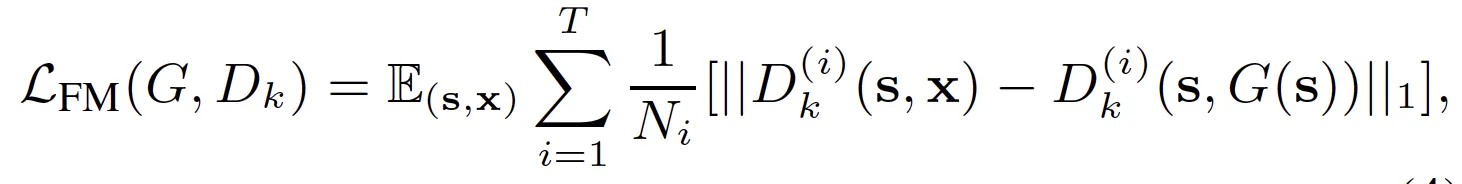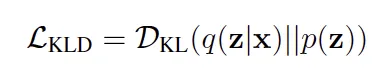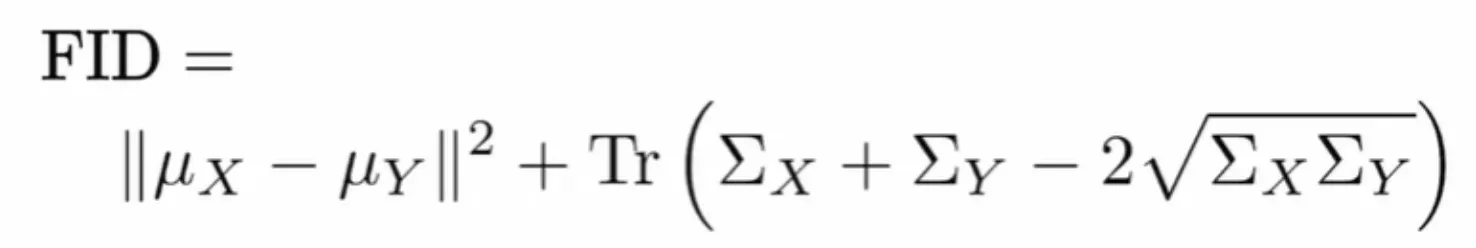Task
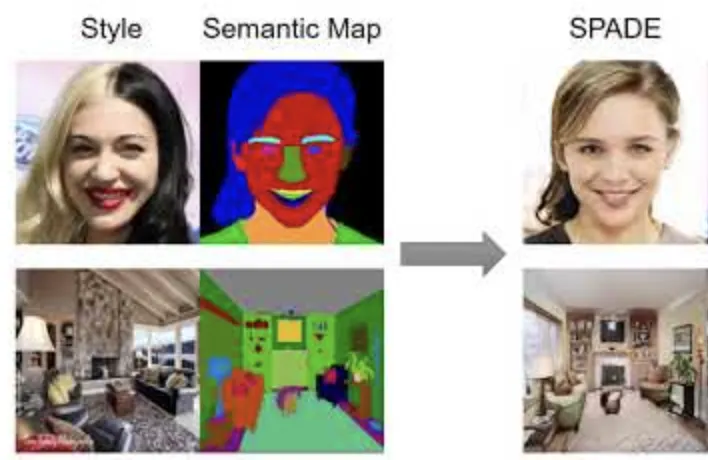
image synthesis from semantic mask
Introduction
Observations
•
semantic awareness가 spatial-adaptiveness보다 더욱 많은 기여를 한다.
•
SPADE에서 와 를 구하기 위해 사용했던 2-layer Conv는 너무 shallow하다.
따라서 같은 semantic class에서는 invariant하게 된다. (distribution의 variance가 감소)
•
Conv 앞 SPADE 블록은 불필요한 연산과 parameter overhead를 야기한다.
Proposing Method
•
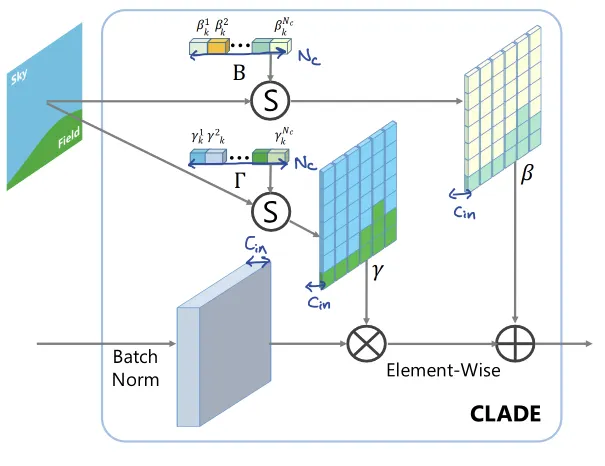
CLADE CLass-Adaptive (DE)Normalization Layer
•
SPADE와 달리, input semantic mask를 class-adaptive하게 사용한다.
•
반면, spatial position, semantic shape, layout of mask에는 의존하지 않는다.
•
이에 더해, spatial-awareness를 위해 position encoding을 적용했다.
Contribution
•
별도의 modulation network가 필요없다.
•
따라서 연산량이 적어졌다.
Related Work
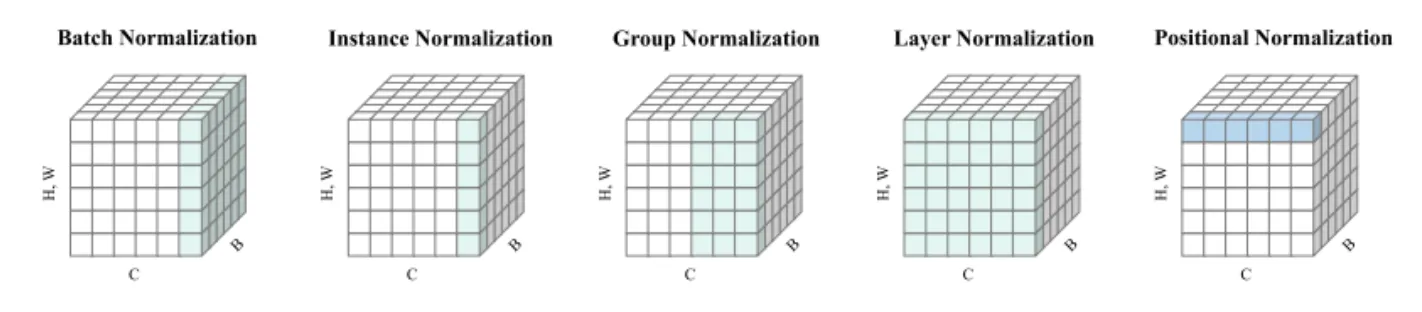
Unconditional Normalization
•
Batch Normalization (BN)
•
Instance Normalization (IN)
•
Group Normalization (GN)
•
Positional Normalization (PONO)
Conditional Normalization
•
Conditional Instance Normalization (Conditional IN)
•
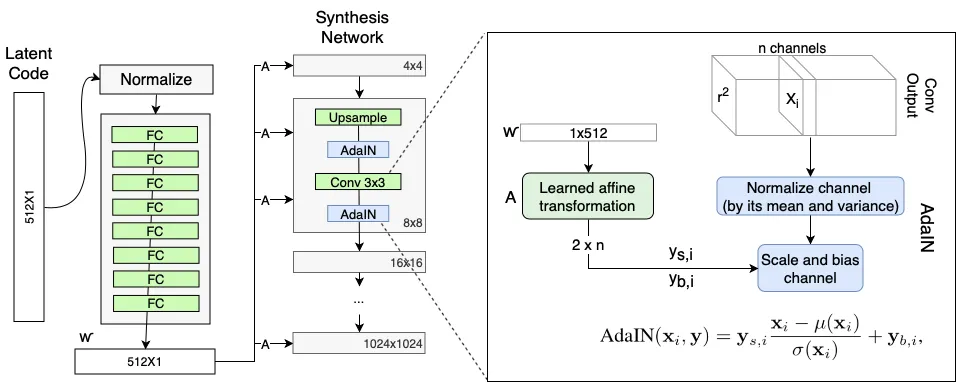
Adaptive Instance Normalization
(AdaIN)
SPADE
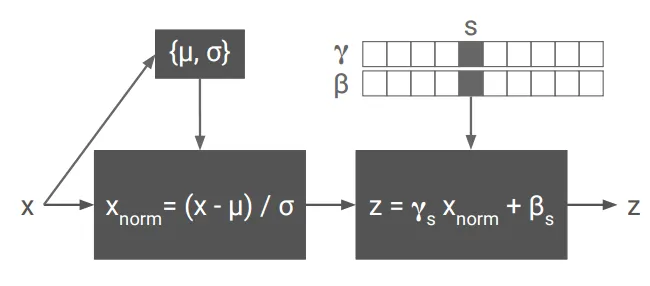
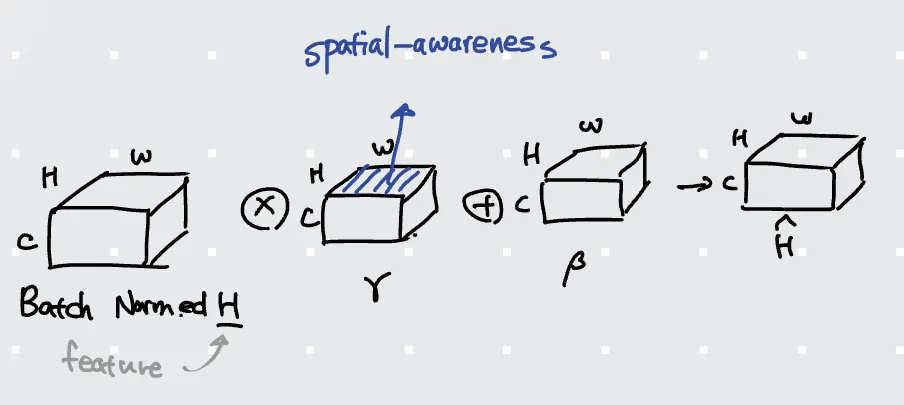
Spatial-adaptiveness
Semantic-awareness
Observations on SPADE
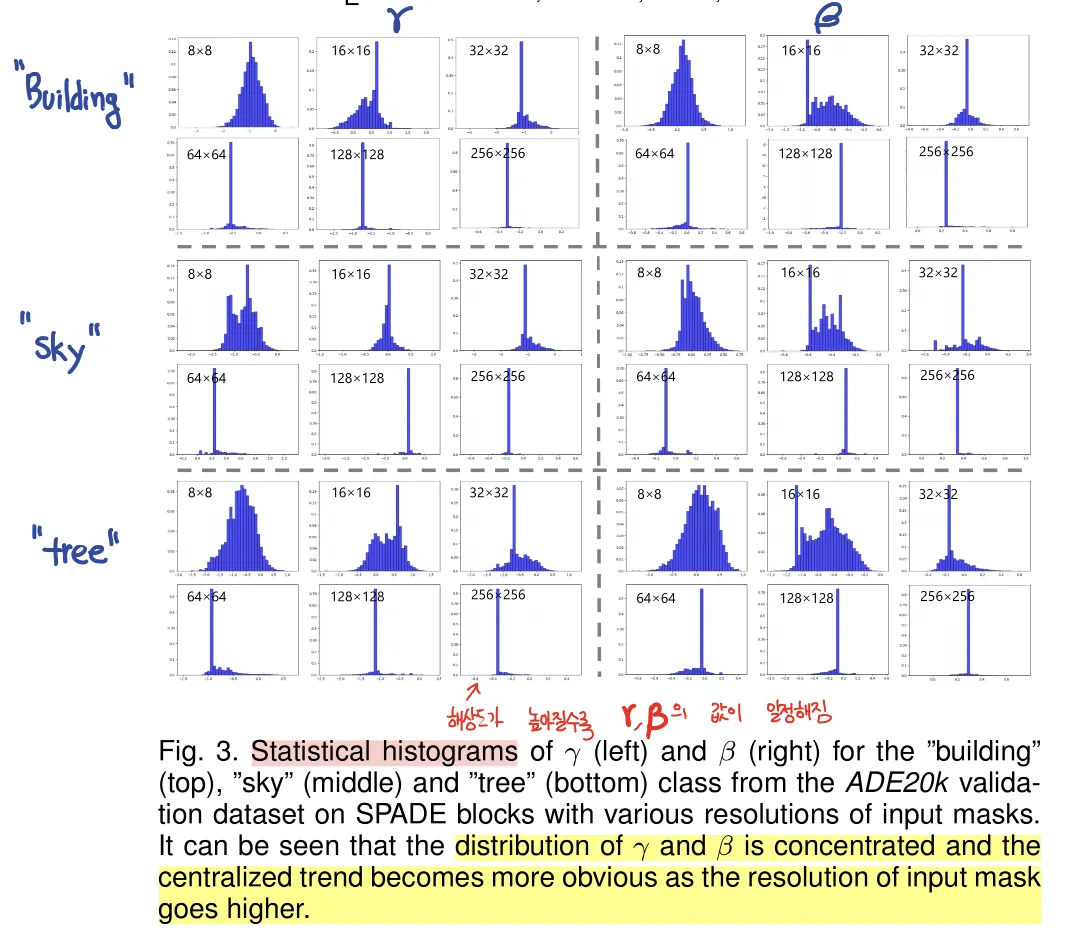
과연 spatial-adaptive 한가요?
고해상도로 갈수록 하나의 값만 나오게 됩니다.
•
spatial-adaptiveness가 깨진다. (특히 고해상도에서)
•
이는 와 를 구하는 modulation network가 너무 얕아서 그렇다. (2-conv layer = shallow!)
•
심지어, 같은 class인 두 물체의 크기가 다르거나 떨어져있어도 동일한 값이 나옵니다.
따라서 이를 개선하는 방법을 제안합니다.
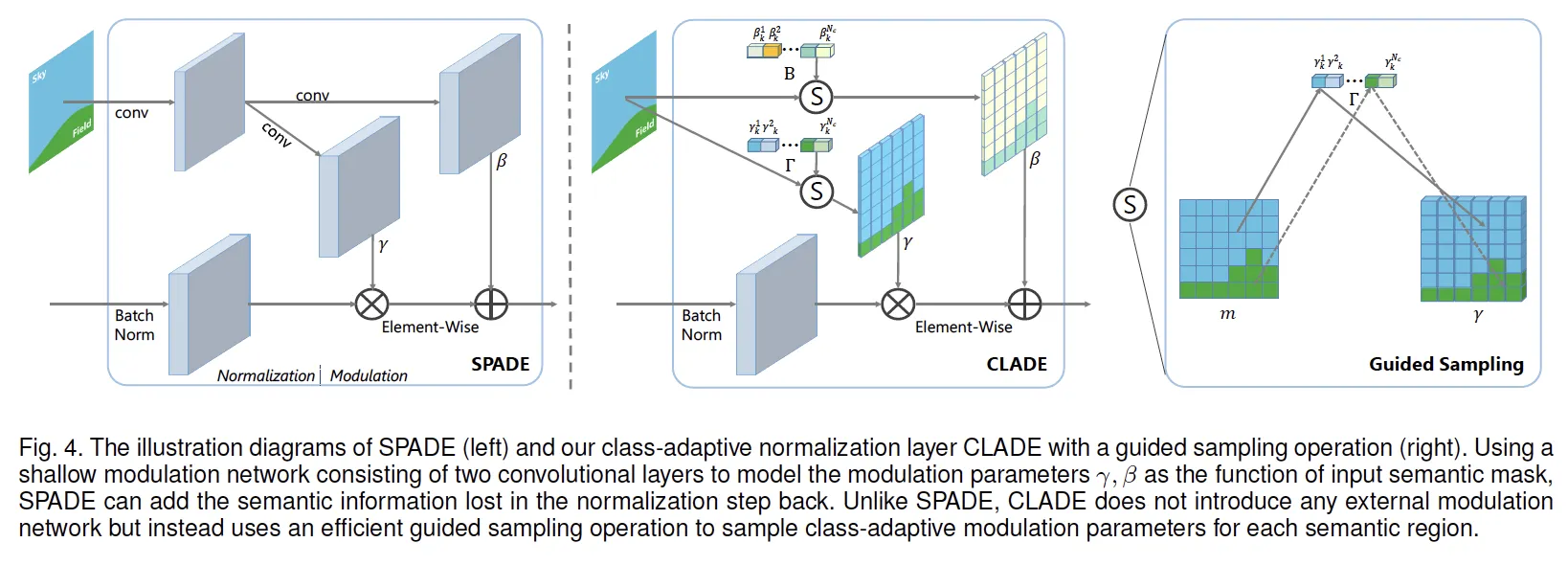
CLADE: Class-Adaptive (DE)Normalization
modulation parameter 는 semantic input 에 adaptive 합니다.
•
SPADE가 pixel-wise spatially adaptive했던 것과 달리,
•
CLADE는 spatial 정보를 의도적으로 무시하고 (spatially-invariant)
오직 semantic class에만 adaptive하게 설계했습니다.
•
따라서 position, size, shape, layout 등 spatial에 관한 어느 것에도 독립적입니다.
이렇게 spatial 정보를 의도적으로 무시한 것은 SPADE의 modulation network 출력이 spatial-adaptive하지 않고 결국 한 값으로 수렴함을 관찰했기 때문에, 이러한 관찰을 바탕으로 이럴바에 그냥 상수값 하나만 잘 쓰자 라고 설계한듯 합니다.
그렇다면 spatial 정보를 의도적으로 무시함으로써 얻는 이점이 무엇이 있을까요?
•
SPADE가 mask를 conv-conv 를 통해 를 구했던 modulation network가 필요없어집니다.
•
CLADE는 이제 각 class에 따른 값을 저장하는 parameter bank만 가지고 있으면 됩니다.
•
따라서 연산량을 줄일 수 있습니다.
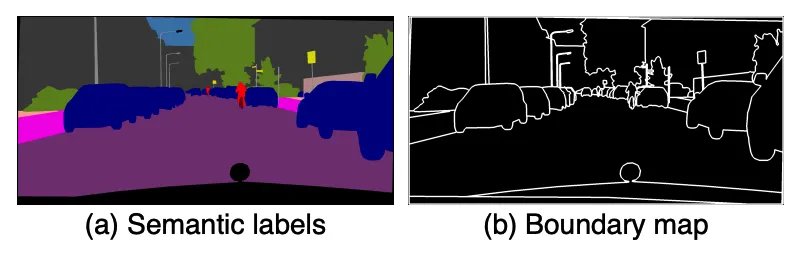
Edge Map: Semantic Label만 있을때 Instance를 구별하는 궁여지책
Semantic Segmentation은 Panoptic Segmentation과 달리 각 Instance에 대한 ID를 구분하지 않습니다.
그렇다면 같은 클래스의 물체가 겹쳐있다면, 어떻게 두 물체를 구분해줄까요?
Pix2PixHD, SPADE처럼 CLADE에서는 Edge Map을 함께 피딩해줍니다.
Edge Map은 경계는 1, 면은 0으로 되어있습니다.
이를 이용해 아래와 같이 Instance간 명확한 경계를 얻을 수 있습니다.
하지만, CLADE는 semantic map을 conv하지 않아 이전 방법처럼 겹쳐서 보내는건 불가능합니다.
따라서 edge map을 먼저 modulation해줍니다.
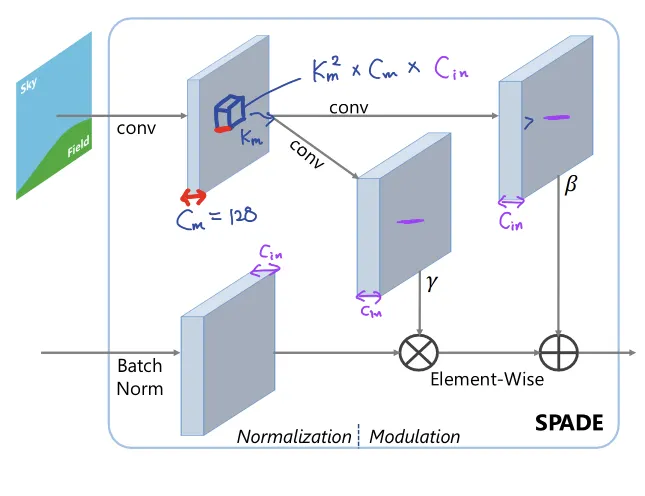
Computation, Parameter Analysis
SPADE
Number of Parameters
•
Params. for conv. layer:
•
Params. for SPADE blk.:
•
Params. Ratio :
FLOPS
•
FLOPs for conv. layer:
•
FLOPs for SPADE block:
•
FLOPs Ratio :
CLADE
Number of Parameters
•
Params for conv layer:
•
Params for CLADE blk:
•
Params Ratio:
FLOPS
•
FLOPs for conv layer:
•
FLOPs for CLADE block:
•
FLOPs Ratio:
•
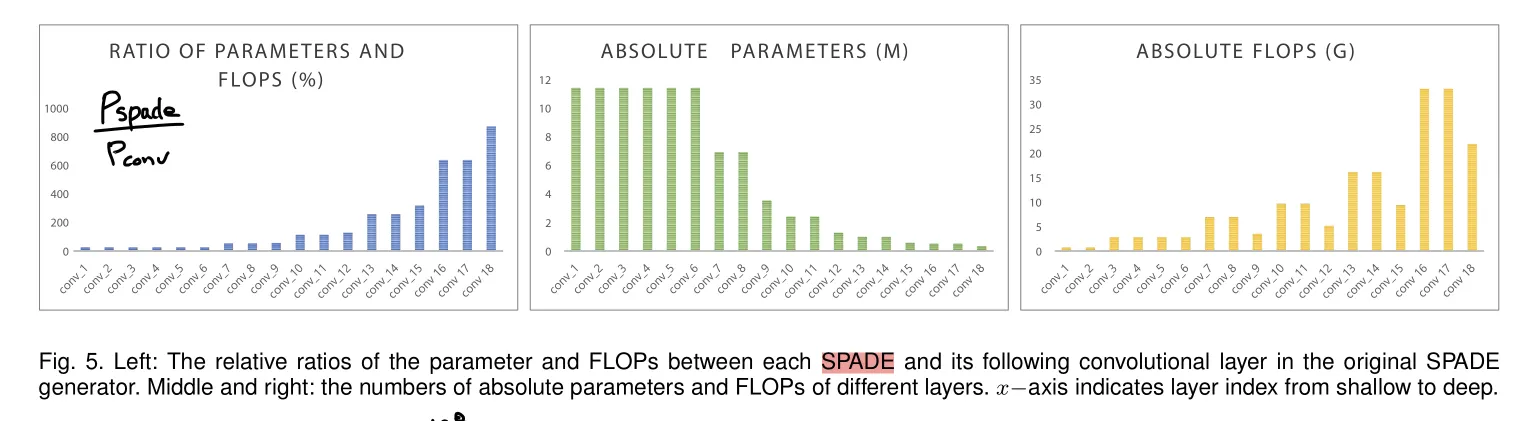
주목할 점은, SPADE에서 고해상도로 갈수록 은 줄어드는 반면 은 128로 고정이기 때문에 overhead가 심하게 나타난다. 이는 연산량의 손해이다. 반면 CLADE에서는 매우 compact한 연산이 가능하다.
•
블록의 파라메터 개수가 매우 적어졌다. SPADE 대비 4.57%로 줄어들었다.
•
블록의 연산량이 매우 적어졌다. SPADE 대비 0.07%로 줄어들었다.
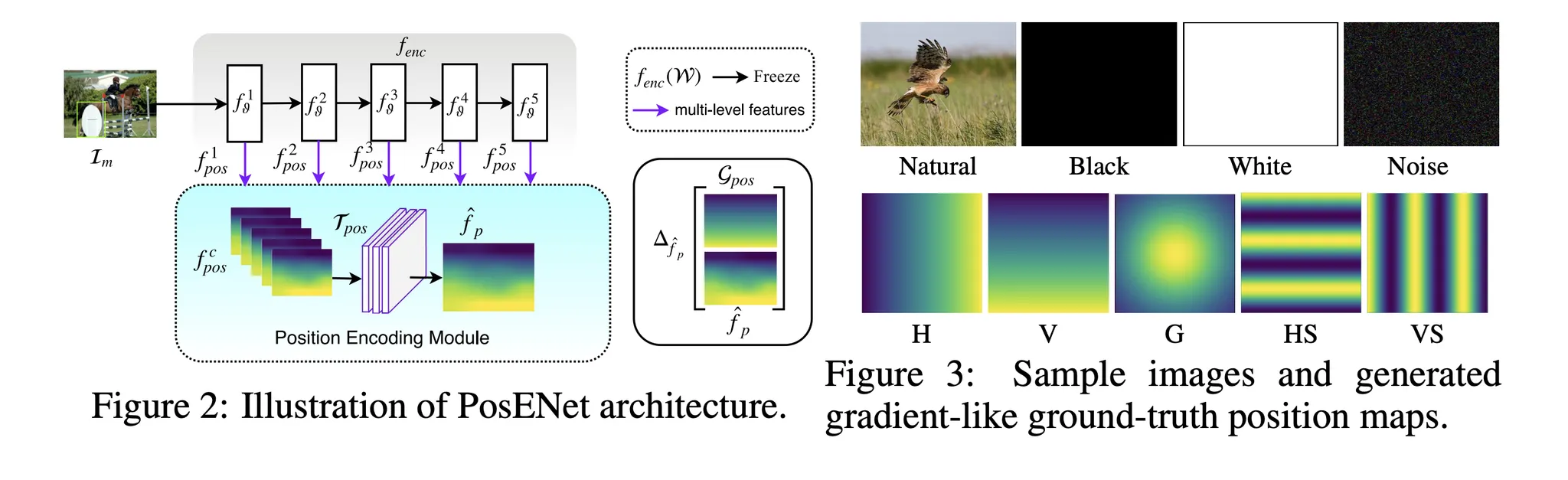
Spatially-adaptive: Position Embedding
•
지금까지는 Semantic Label map의 label에 따라 Bank에서 값을 찾아 broadcasting해주었습니다.
•
이는 spatial 정보를 전혀 담고 있지 않습니다.
•
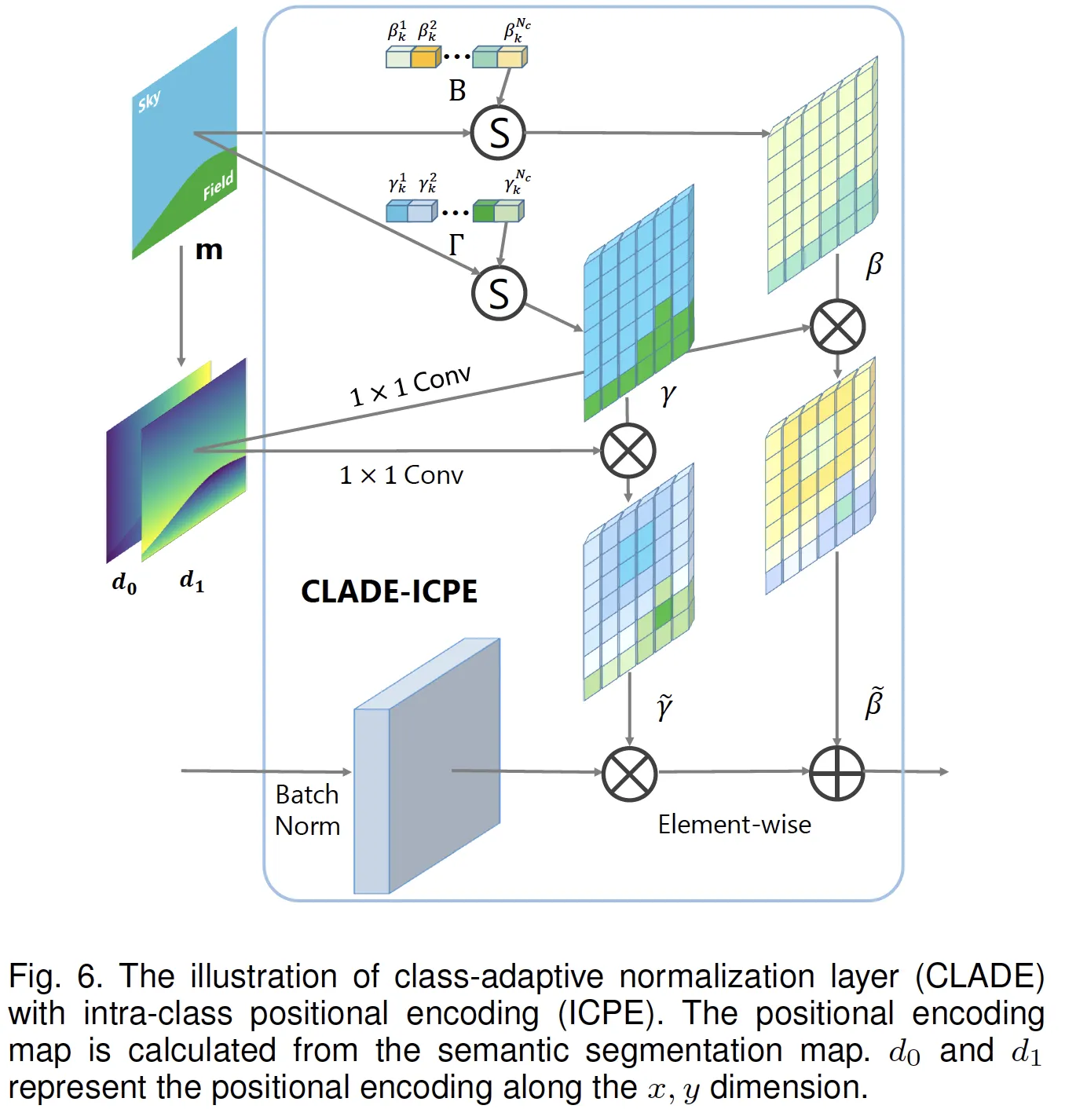
parameter를 가져온 이후에 position 정보를 encoding해주었습니다.
•
이는 position 정보가 학습되는 sementic의 statistic에 영향을 미쳐서는 안되기 때문이라고 생각됩니다.
즉, 자동차는 작게있으나 크게있으나 같은 모양을 띄어야 한다는 뜻입니다.
•
Position embedding은 object center에 대한 상대거리로 정의됩니다.
each pixel
semantic category
semantic object
object center
encoding map
•
Distance Map
maximum offset
•
normalized distance map
•
1X1 conv. to map modultation parameters
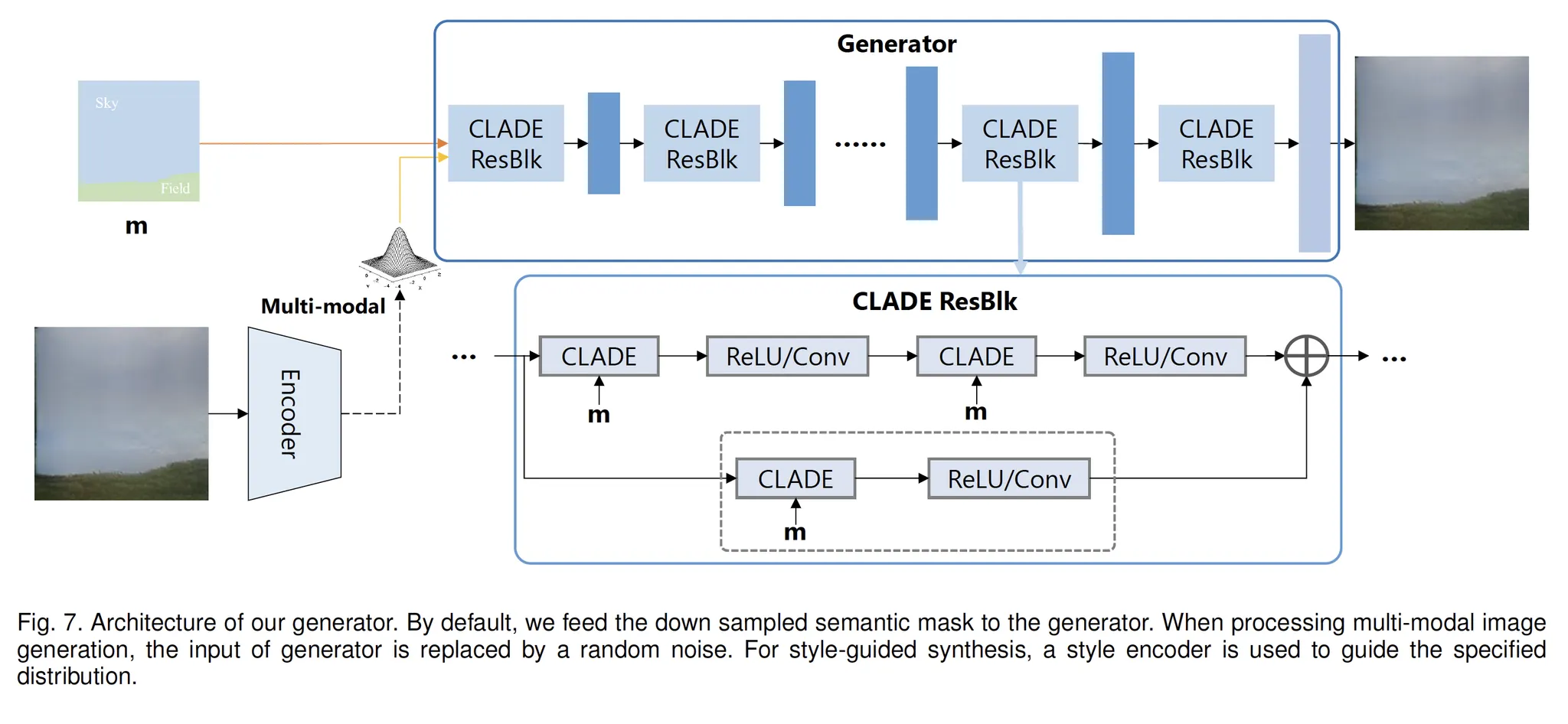
CLADE Generator
•
기본적으로, SPADE의 Generator를 따릅니다.
Encoder for multi-modal synthesis
다른 이미지로부터 Style을 추출하기 위해 Encoder를 디자인합니다.
Encoder는 여러개의 conv-IN-LReLU 블록으로 이루어집니다.
Encoder Output은 mean과 variance vector 두개로 나옵니다.
이를 이용해 만들어진 분포를 이용하여 Random Vector를 샘플링하고, 이를 CLADE에 넣어 style guidance로 사용합니다.
Experiments
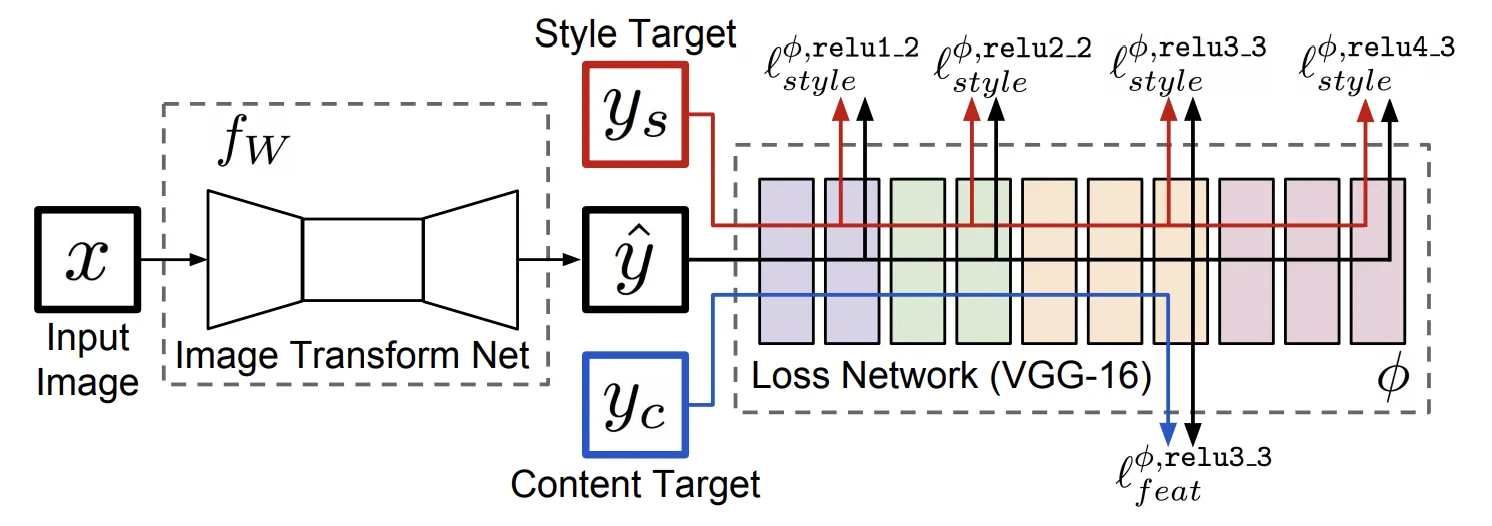
Loss
Generator Loss
Todo: Why Hinge Loss is better?
2. D Feature Matching Loss between real and synthesized image (Multi-scale D)
4. : KL Divergence Loss
(Multi-modal synthesis only)
Experiments Setting and Parameters
Datasets
ADE-20k
ADE20k-outdoor
COCO-Stuff
150 categories | 20,210 train | 2k val | 3k test
subset of ADE20k I 9,649 train | 943 val
182 categories | 118,000 train | 5,000 val
•
Diversity categories and small objects
Cityscapes
35 categories | 2,975 train | 500 val
•
High-Resolution Images
CelebAMask-HQ
19 classes | 30,000 masks from CelebAHQ
DeepFasionSMIS
30,000 train | 2,247 val
Evaluation Metrics
•
Segmentation on synthesized image
Algorithms for each datasets
1. mean IoU (mIoU)
2. Pixel accuracy (accu)
3. Frechet Inception Distance (FID)
•
낮은 FID -> 두 분포의 거리가 가깝다 -> 진짜와 가짜가 유사하다
•
Measure the distribution distance between synthesized images and real images
•
Calculate FID between ..
- generated validation images and real training images (not real validation image!)
- 왜냐하면 training 이미지가 val image보다 더 많기 때문에 real 이미지의 분포 특성을 더욱 잘 반영하기 때문입니다.
4. User Study
•
사람에게 CLADE와 비교알고리즘 결과를 나란히 놓고 "어느 것이 더 진짜같은지" 물어보았습니다.
•
20명에게 40개의 결과를 보여주어 설문하였습니다.
•
샘플이 너무 작아 의미가 있나 싶습니다.
•
결과도 인상적이지 않습니다. 그냥 우리 이런것도 했다 정도..
실험 1: Qualitative Result
결과입니다.
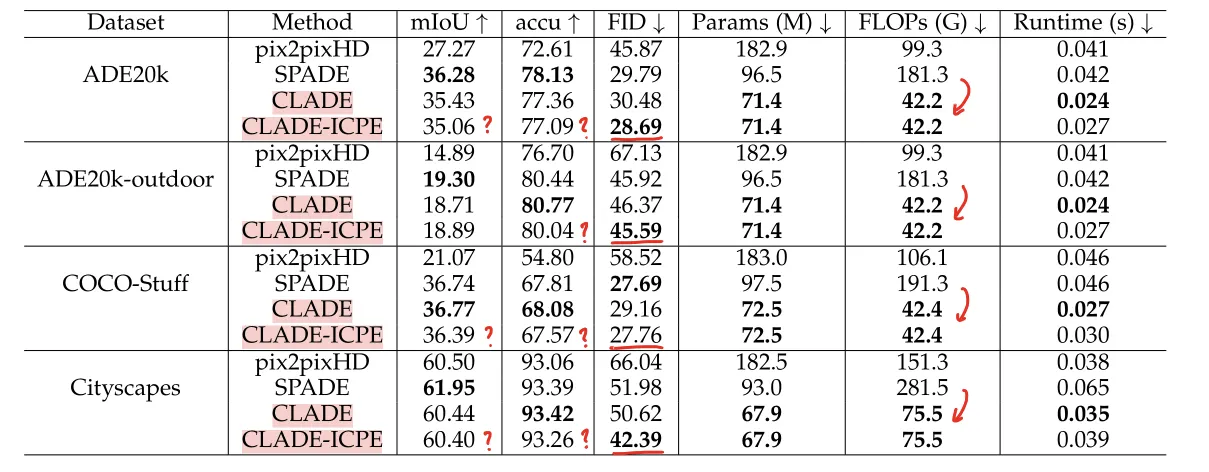
CLADE 가 position encoding 없는 버전, CLADE-ICPE가 position encoding 한 버전인데, 두가지 특징을 보여주고 있습니다.
•
생성된 이미지에 대한 Segmentation 결과는 SPADE에 앞서거니 뒤서거니 합니다.
•
Position Encoding은 FID Score에서 우수한 성능을 보여주었습니다.
이는 Generator가 더욱 실제같은 이미지를 생성한다는 뜻입니다.
•
Position Encoding은 Segmentation 결과에 큰 영향을 미치지 못했습니다.
오히려 안하느니만 못한(?) 결과도 나왔습니다.
•
성능에서 큰 향상이 없는 대신 (당연합니다. 이 논문이 애초에 "가 하나로 나오잖아. 그럼 상수로 만들면 되지!" 라는 발상에서 시작했으니) Parameter 수, FLOPs 그리고 Runtime에서 큰 향상이 있었습니다.
실험 2: Qualitative Result
실험 3: Multi-modal and Style-Guided Synthesis
•
별도의 Encoder를 이용해 한 이미지로부터 스타일에 관여하는 parameter를 뽑고
•
Distribution으로부터 랜덤한 Style Vector를 샘플링 한 후
•
다른 semantic mask에 이미지를 생성하는 Style Transfer 실험입니다.
•
첫번째 열은 같은 Semantic mask에 Nosie Vector로부터 생성된 다양한 이미지들이고
•
두번째 열은 Reference Image로 만든 Distribution에서 샘플링한 Vector로 생성한 이미지입니다.
•
"잘 된다"
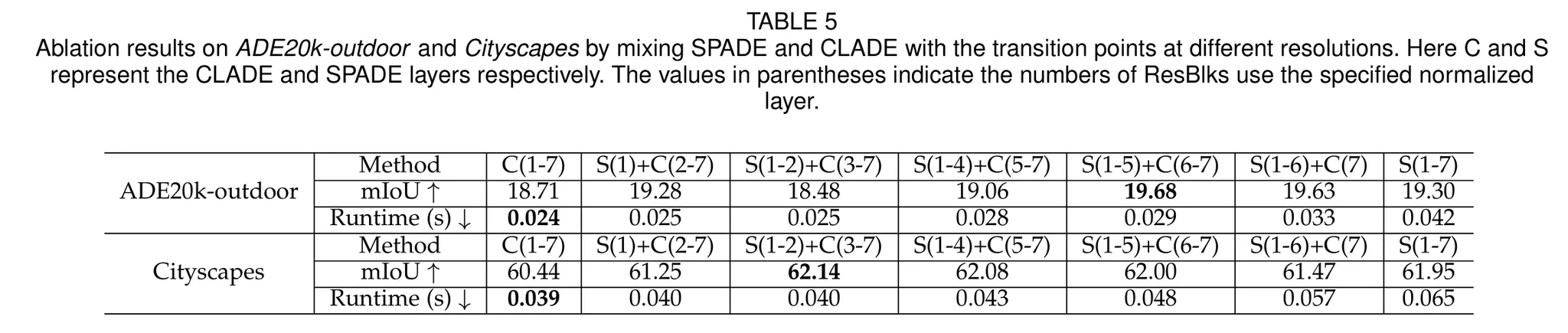
실험 4: SPADE + CLADE?
•
Low Layer 에서는 parameter의 distribution이 존재하니 SPADE를 쓰고
•
Top Layer 에서는 어차피 상수로 collapse되니 CLADE를 써보기로 합니다.
•
둘을 같이 쓰면 성능이 더 좋아진다고 합니다.
•
그런데 왜 SPADE의 span이 더 넓은데, pure SPADE보다 성능이 증가하는 걸까요?
•
class 별로 명시적인 bank를 따로 둔 만큼, 암묵적인 channel 연산보다는 성능이 좋다는 건가..
실제로 돌려봐야겠습니다.
실험 5: Positional Encoding?
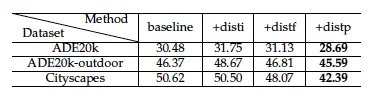
저자에 따르면 spatial 정보를 제공하는 것은 물론 중요하지만, Position Encoding은 신중하게 잘 설계해야 하고 그렇지 않을경우 성능을 해칠수도 있다고 합니다. 저자는 세가지 방법을 실험했습니다.
•
+disti Positional Encoding Map → Concat with Downsampled Semantic map
•
+distf Positional Encoding Map → 1X1 Conv → Concat with Normalized Feature
•
+distp (본문) Positional encoding map으로 Semantic-adaptive modulation parameter를 modulate
Metric은 FID ↓입니다.
결과를 통해 다음을 알 수 있습니다.
•
+disti 직접 concat하면, 안하느니만 못하다.
•
+distf 직접 concat하는 것보다 feature에 제공하는 것이 조금 더 낫다. (여전히 안하느니만..)
•
+distp 그래도 element-wise multiplication이 가장 좋더라.
실험 6: Generalization Ability
•
기존 SPADE를 활용한 방법들에서 SPADE→CLADE로 교체하고 실험을 했다.