//
Search
🤖

Transformers, 수학과 코딩으로 이해하기

1: Introduction

1.1: Transformers 개요

트랜스포머 아키텍처는 Vaswani 등 이 발표한 논문 "Attention is All You Need"에서 소개되었으며, 특히 자연어 처리(NLP)에서 딥 러닝을 혁신했습니다. 트랜스포머는 자기 어텐션 메커니즘 (Self-attention mechanism) 을 사용하여 입력 시퀀스를 한 번에 처리할 수 있습니다. 이 병렬 처리는 더 빠른 계산과 데이터 내 장기 의존성의 효과적인 관리가 가능합니다. 먼저 트랜스포머의 구조를 간략히 살펴보겠습니다.
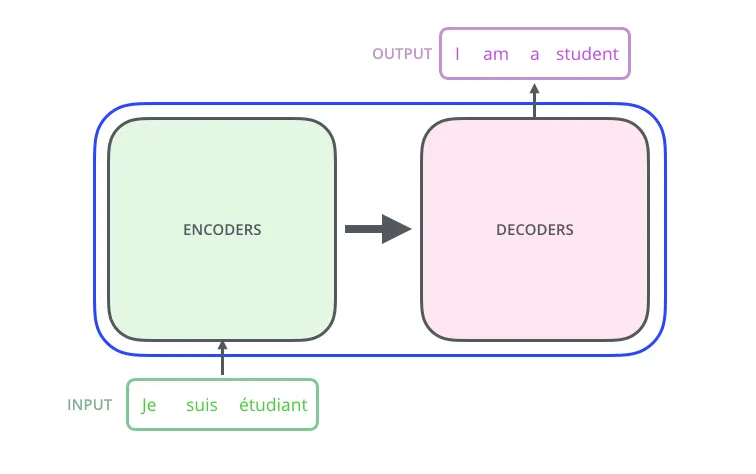
Credit: The Illustrated Transformer – Jay Alammar
가장 먼저, Transformer를 블랙박스로 생각해보겠습니다. 입력 시퀀스를 받아 새로운 출력 시퀀스를 만들게 됩니다.
Credit: The Illustrated Transformer – Jay Alammar
트랜스포머는 인코더와 디코더 두 부분으로 구성됩니다.
•
인코더는 입력 시퀀스를 처리하여 연속적인 표현을 생성합니다.
•
디코더는 이 표현으로부터 출력 시퀀스를 생성합니다.
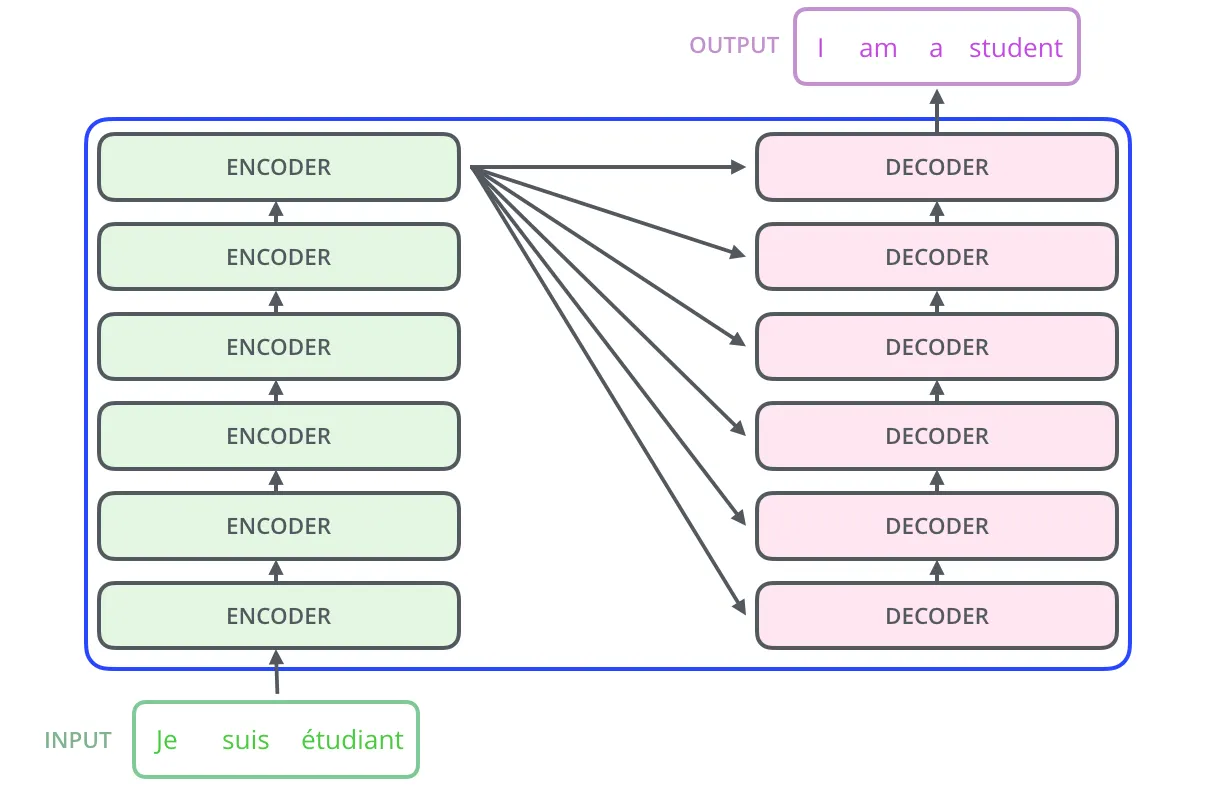
이러한 인코더는 여러 층으로 구성되며, 각각 디코더 레이어와 연결되어 있습니다. 모든 인코더 층의 구조는 같습니다.
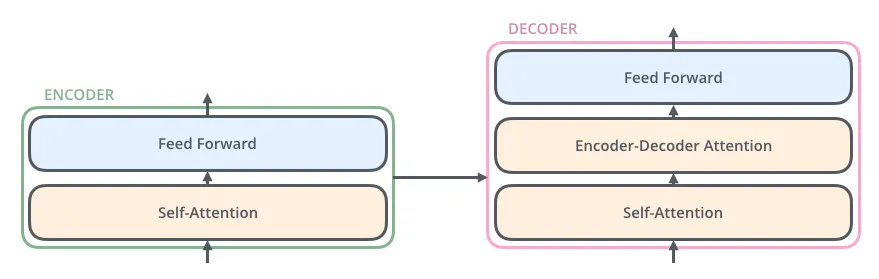
이러한 인코더는 두개의 서브 레이어로 구성되어 있고, 디코더는 세개의 레이어로 구성되어 있습니다.
인코더와 디코더의 차이는 간단합니다. 디코더에는 인코더의 출력을 통합하는 어텐션 층이 있다는 것입니다.
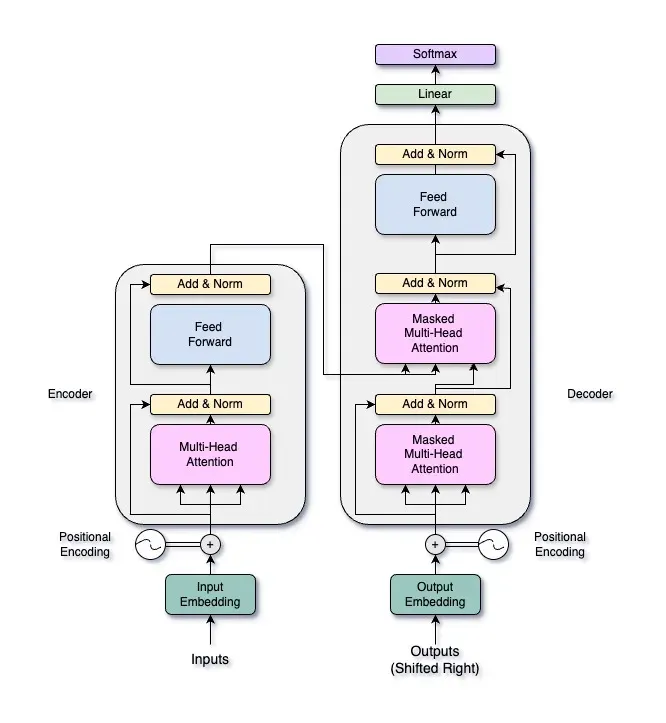
따라서 Transformers의 전체 구조는 다음과 같습니다.
인코더와 디코더는 여러 층으로 구성되며, 각각 다중 헤드 자기 어텐션 메커니즘 (a multi-head self-attention mechanism) 과 위치별 피드 포워드 네트워크(position-wise feed-forward network)를 포함합니다. 이번 글에서는 다중 헤드 어텐션 메커니즘에 집중할 것이며, 향후 글에서 전체 트랜스포머 아키텍처를 탐구할 것입니다.
만약 이 구조가 익숙하지 않다면, 아래 블로그 포스트를 훑어보시길 추천드립니다. (English) The Illustrated Transformer (Korean) The Illustrated Transformer

1.2: Multi-Head Attention Overview

다중 헤드 어텐션(Multi-Head Attention)은 모델이 입력 시퀀스의 여러 부분에 동시에 집중하여 다양한 데이터를 포착할 수 있게 합니다. 이를 무대의 여러 부분을 비추는 여러 스포트라이트로 생각해보세요. 각 스포트라이트(또는 '헤드')가 다른 공연자(또는 데이터 특징)를 비추어 관객(또는 모델)이 전체 장면을 더 명확하게 볼 수 있게 합니다. 입력을 여러 하위 공간(subspaces)으로 나누어 각 하위 공간마다 어텐션 메커니즘을 적용함으로써 다중 헤드 어텐션은 모델에 입력 데이터의 여러 관점을 제공합니다. 이 설정은 모델이 데이터 내 복잡한 관계를 더 효과적으로 이해할 수 있게 합니다.
이 메커니즘은 트랜스포머가 시퀀스의 다양한 부분에 주의를 기울여 데이터 내 다양한 관계를 포착할 수 있게 합니다. 이는 여러 입력 관점을 제공하여 학습 과정을 개선하고 모델의 일반화 능력을 향상시킵니다. 또한, 입력 데이터를 동시에 학습할 수 있어 모델의 표현력을 높입니다.
이러한 기능 덕분에 다중 헤드 어텐션은 언어 번역에서 이미지 처리에 이르기까지 다양한 응용 분야에서 트랜스포머 모델의 성공에 중요한 요소가 됩니다.

2: Mathematical Foundations

2.1: Attention Mechanism

신경망의 어텐션 메커니즘은 데이터를 처리하는 동안 특정 부분에 집중하는 인간의 능력을 모방하도록 설계되었습니다. 책을 읽을 때, 눈은 페이지의 모든 단어에 동일하게 주의를 기울이지 않습니다. 대신 이야기 이해에 도움이 되는 중요한 단어에 더 집중합니다. 이와 유사하게, 신경망에서 어텐션은 모델이 다른 입력 요소의 중요성을 동적으로 가중치를 두어 우선순위를 정할 수 있게 합니다. 이를 통해 언어 번역, 텍스트 요약 등의 작업에서 모델의 성능을 향상시킬 수 있습니다.
수학적으로 어텐션 메커니즘은 쿼리(Query), 키(Key), 값(Value) 집합을 사용하여 설명할 수 있습니다.
1.
입력 데이터에 Linear Transformation을 통해 집합 Q, K, V\textbf{Q, K, V}를 얻습니다.
2.
어텐션 점수는 각 쿼리 (qq) 와 모든 키들 (k1,k2,⋯ ,kn)k_1, k_2,\cdots,k_n)의 dot product로 계산됩니다:
score(q,ki)=q⋅ki\text{score}(q,k_i)=q\cdot k_i
이것은 문장에서 각 단어 (키) 집중하고자 하는 단어 (쿼리)와 얼마나 유사한지 측정합니다. 점수가 높을 수록 더 유사합니다.
3.
키의 차원이 높을수록 어텐션의 점수가 커지게 됩니다. 따라서 dot product가 너무 커지는 것을 방지하기 위해, 점수를 스케일링합니다. 이때 키의 차원에 대한 sqare root (dk\sqrt{d_k})를 스케일링 계수로 사용합니다.
scaled_score(q,ki)=q⋅kidk\text{scaled\_score}(q,k_i)=\frac{q\cdot k_i}{\sqrt{d_k}}
이는 무대의 크기에 따라 스포트라이트의 강도를 조절하는 것과 비슷합니다. 이렇게 하면 점수가 관리 가능하게 유지되고 훈련 중에 안정적인 기울기를 유지할 수 있습니다. 이 스케일링은 소프트맥스 함수로 전달되는 값의 표준 편차가 1에 가깝게 하여 학습 중에 안정적인 기울기를 유지하도록 도와줍니다.
왜 이것이 필요한지 이해하기 위해 내적과 고차원 벡터의 특성을 고려해 봅시다. 차원 dkd_k인 두 벡터 qq와 kik_i의 내적을 계산할 때, 내적의 기대값은 dkd_k에 비례합니다. 스케일링 없이 dkd_k가 증가하면 내적의 분산이 커져서 매우 큰 값이 되고 소프트맥스 함수가 거의 이진 출력(즉, 0이나 1에 가까운 확률)을 생성하게 됩니다. 이러한 급격한 변화는 기울기(gradient)를 매우 작게 만들어 모델의 효과적인 학습을 저해합니다.
내적을 dkd_k로 나누어 소프트맥스 함수의 입력을 정규화하여 점수가 적절한 범위 내에 유지되도록 합니다. 이 정규화는 모델이 균형을 유지하면서 더 효과적이고 안정적으로 학습할 수 있게 합니다.
4.
이 스케일된 점수는 소프트맥스 함수를 거쳐 어텐션 가중치로 변환됩니다. 소프트맥스 함수는 점수를 확률로 변환하여 쿼리에 대한 각 키의 중요도를 나타냅니다:
attention_weight(q,ki)=exp⁡(scaled_score(q,ki))∑j=1n(scaled_score(q,ki))\text{attention\_weight}(q,k_i ) =\frac {\exp\left(\text{scaled\_score}(q, k_i)\right)} {\sum^n_{j=1}\left( \text{scaled\_score}(q, k_i)\right)}
이 단계는 조정된 스포트라이트 강도를 명확한 순위로 변환하여 장면의 가장 관련 있는 부분을 더 밝게 강조하는 것과 비슷합니다.
5.
최종 어텐션 출력은 어텐션 가중치를 사용하여 값의 가중 합을 취함으로써 얻어집니다:
attention_output=∑i=1nattention_weight(q,ki)⋅vi\text{attention\_output}=\sum^n_{i=1}\text{attention\_weight}(q,k_i) \cdot v_i
여기서 viv_i는 키 kik_i에 해당하는 값을 나타냅니다. 이 가중 합은 책의 가장 중요한 부분에 집중하여 이야기를 더 잘 이해하는 것처럼, 값들 중 가장 관련성이 높은 정보를 결합합니다.

2.2: 다중 헤드 어텐션 (Multi-Head Attention)

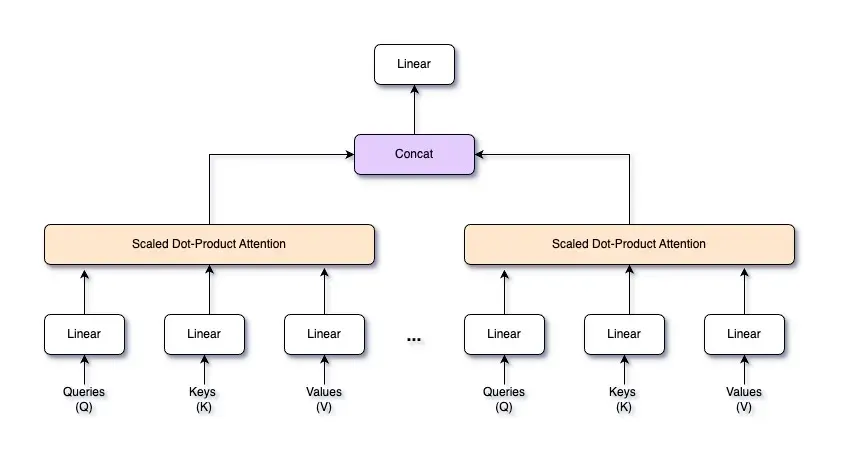
다중 헤드 어텐션은 입력 시퀀스의 다양한 부분에 동시에 집중하여 데이터 내 여러 관계를 포착할 수 있는 고급 어텐션 메커니즘입니다. 단일 어텐션 메커니즘 대신, 입력을 여러 "헤드"로 나누어 각 헤드가 독립적으로 쿼리(Q), 키(K), 값(V) 집합을 가지고 어텐션 작업을 수행하며, 그 출력은 결합됩니다. 이는 모델이 데이터 내 복잡한 패턴과 의존성을 이해할 수 있게 합니다.
복잡한 장면을 이해하려고 할 때, 여러 쌍의 눈이 각각 다른 부분을 본다면 더 포괄적인 이해를 얻을 수 있는 것과 유사합니다. 다중 헤드 어텐션도 마찬가지로 모델이 입력 데이터의 다른 부분에 동시에 집중할 수 있게 하여 더 풍부하고 세부적인 표현을 제공합니다.
입력 시퀀스 X\mathbf{X}가 주어지면, 학습된 선형 변환을 통해 쿼리 Q\mathbf{Q}, 키 K\mathbf{K}, 값 V\mathbf{V}로 투영합니다. 각 헤드 ii 에 대해 별도의 가중치 행렬 WQ,WK,WV\mathbf{W_Q, W_K, W_V}를 가집니다.
Qi=XWiQ,Ki=XWiK,Vi=XWiVQ_i=XW_i^Q,\quad K_i=XW_i^K,\quad V_i=XW_i^V
이 투영은 각 헤드가 입력 데이터의 다른 측면에 집중할 수 있게 합니다. 각 헤드 ii 에 대해 스케일된 점곱 어텐션 메커니즘(scaled dot-product attention mechanism) 을 사용하여 어텐션 점수를 계산합니다. 헤드 ii의 어텐션 출력은 다음과 같습니다:
Attention Output=softmax(QKTdk)V\text{Attention Output} = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V
여기서 dkd_k는 키 벡터의 차원으로, 점수가 적절히 스케일되도록 합니다.
모든 헤드의 어텐션 출력을 계산한 후, 특징 차원에 따라 결합합니다. 만약 hh개의 헤드가 각각 dvd_v 차원의 출력을 생성하면, 결합된 출력은 h×dvh \times d_v 차원을 갖습니다.
MultiHead(Q, K, V)=Concat(head1,…,headh)\text{MultiHead(Q, K, V)} = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)
결합된 출력은 학습된 가중치 행렬 WOW^O를 사용하여 원래 입력 차원 dd로 다시 투영됩니다:
Output=MultiHead(Q, K, V)WO\text{Output} = \text{MultiHead(Q, K, V)} W^O
다중 어텐션 헤드를 결합하는 핵심 아이디어는 모델이 입력 시퀀스에서 동시에 다양한 유형의 정보를 포착할 수 있게 하는 것입니다. 여러 헤드를 사용하면 각 헤드가 입력의 다른 부분 또는 다른 특징에 주목할 수 있습니다. 이러한 어텐션의 다양성은 데이터의 더 풍부하고 세밀한 표현을 제공합니다.

2.3: Position-wise Feed-Forward Networks

트랜스포머 아키텍처에서 각 층은 다중 헤드 어텐션 메커니즘과 그 다음 위치별 피드 포워드 네트워크로 구성됩니다. 이러한 피드 포워드 층들은 시퀀스의 각 위치에 독립적으로 적용되므로 "위치별 (Position-wise)"이라는 용어가 사용됩니다. 기본적으로 이는 입력 시퀀스의 각 위치에 별도로 동일하게 적용되는 단순 완전 연결 신경망 (Fully-conntected Network) 입니다.
예를 들어, 한 공장을 상상해보세요. 이 공장은 컨베이어 벨트 위의 각 제품이 동일한 기계를 거칩니다. 이때 각 기계는 제품을 특정 방식으로 처리하여 새로운 것을 추가하거나 정제합니다. 이와 마찬가지로, 시퀀스의 각 위치는 피드 포워드 층에 의해 독립적으로 처리되어 표현을 변환하고 향상시킵니다.
이 피드 포워드 층의 목적은 모델에 비선형성과 추가 학습 용량을 도입하는 것입니다. 어텐션 메커니즘이 시퀀스의 다른 부분에서 정보를 집계한 후, 피드 포워드 네트워크는 이 정보를 처리하여 표현을 더욱 변환하고 정제합니다.
수학적으로, 위치별 피드 포워드 네트워크는 두 개의 선형 변환과 그 사이에 ReLU\text{ReLU} 활성화 함수를 포함합니다. 특정 위치에서 입력 xx가 주어지면, 피드 포워드 네트워크는 다음과 같이 표현할 수 있습니다:
FFN(x)=max⁡(0,xW1+b1)W2+b2\text{FFN}(x)=\max(0, xW_1+b_1)W_2+b_2
여기서:
•
W1W_1과 W2W_2는 학습된 가중치 행렬입니다.
•
b1b_1과 b2b_2는 학습된 바이어스 벡터입니다.
•
max⁡(0,xW1+b1)\max(0, xW_1+b_1)는 요소별로 적용된 ReLU 활성화 함수를 나타냅니다.
1.
입력 xx는 먼저 가중치 행렬 𝑊1𝑊_1과 바이어스 𝑏1𝑏_1을 사용하여 선형 변환됩니다:
x1=xW1+b1x_1=xW_1+b_1
이 단계를 공장으로 비유하자면, 입력이 학습된 가중치와 바이어스를 기반으로 초기 수정을 거치는 첫 번째 기계를 통과하는 과정입니다.
2.
선형 변환 후에는 비선형성을 도입하는 ReLU 활성화 함수가 뒤따릅니다:
x2=max⁡(0,x1)x_2=\max(0,x_1)
ReLU(Rectified Linear Unit, 정류 선형 유닛)은 모든 음수 값을 0으로 설정하여 모델이 데이터의 비선형 관계를 포착할 수 있게 합니다. 이 단계는 첫 번째 기계에서 양의 기여만 통과시키는 것과 같습니다.
3.
활성화된 출력은 두 번째 가중치 행렬 𝑊2𝑊_2과 바이어스 𝑏2𝑏_2를 사용하여 다시 선형 변환됩니다:
FFN(x)=x2W2+b2\text{FFN}(x)=x_2W_2+b_2
이 마지막 단계는 최종 출력을 더 정제하는 것으로, 두 번째 기계에서 추가 수정을 통해 완성된 제품을 생산하는 것과 같습니다.
트랜스포머 아키텍처의 위치별 피드 포워드 네트워크 (position-wise feed-forward network)는 다중 헤드 어텐션 메커니즘이 포착한 정보를 더 처리합니다. 어텐션 메커니즘이 시퀀스의 다른 부분에 집중하고 문맥별 정보를 집계하는 동안, 피드 포워드 네트워크는 각 위치에서 이 정보를 정제하고 변환하여 모델이 복잡한 패턴과 의존성을 더 잘 포착할 수 있게 합니다.

3: Multi-Head Attention 직접 코딩해보기.

이 섹션에서는 Python과 numpy를 사용하여 다중 헤드 어텐션 메커니즘을 처음부터 구현하는 방법을 알아보겠습니다. 목표는 입력이 과정 중에 어떻게 처리되는지 이해하는 것입니다.

3-1: Multi-Head Attention 클래스 정의.

우선, 다중 헤드 어텐션 메커니즘에 필요한 매개변수를 관리하는 MultiHeadAttention 클래스를 정의합니다. 각 단계별로 설정 방법을 알아보겠습니다.
import numpy class MultiHeadAttention: def __init__(self, num_hiddens, num_heads, dropout=0.0, bias=False): self.num_heads = num_heads self.num_hiddens = num_hiddens self.d_k = self.d_v = num_hiddens//num_heads
Python
복사
초기화 메서드에서는 모델의 어텐션 헤드 수와 총 히든 유닛 수를 먼저 설정합니다. 이 값들은 클래스 인스턴스화 시 인수로 제공됩니다.
•
num_hiddens: 모델의 총 히든 유닛 수를 나타냅니다. 이는 입력 데이터에 적용되는 선형 변환의 크기를 결정하는 중요한 매개변수입니다.
•
num_heads: 어텐션 헤드의 수를 나타냅니다. 각 헤드는 입력의 다른 부분에 독립적으로 집중하여 모델이 데이터의 다양한 측면을 포착할 수 있게 합니다.
•
dropout: 드롭아웃 비율로, 이 구현에서는 사용되지 않지만 완전성을 위해 포함되어 있습니다.
•
bias: 선형 변환에 바이어스 항을 포함할지 여부를 나타내는 불리언 플래그입니다.
그런 다음 각 헤드의 쿼리와 값의 차원을 계산합니다. 총 히든 유닛 수(num_hiddens)가 모든 헤드(num_heads)에 걸쳐 나뉘므로, 각 헤드는 num_hiddens // num_heads 차원의 쿼리와 값을 갖습니다.
self.W_q = np.random.rand(num_hiddens, num_hiddens) self.W_k = np.random.rand(num_hiddens, num_hiddens) self.W_v = np.random.rand(num_hiddens, num_hiddens) self.W_o = np.random.rand(num_hiddens, num_hiddens)
Python
복사
다음으로 쿼리, 키, 값, 출력 변환을 위한 가중치 행렬을 초기화합니다. 이 가중치 행렬은 무작위로 초기화됩니다.
•
W_q: 입력 데이터를 쿼리로 변환하는 데 사용됩니다. 이는 입력 특징을 쿼리 공간으로 매핑합니다.
•
W_k: 입력 데이터를 키로 변환하는 데 사용됩니다. 이는 입력 특징을 키 공간으로 매핑합니다.
•
W_v: 입력 데이터를 값으로 변환하는 데 사용됩니다.
•
W_o: 모든 헤드의 연결된 출력을 원래 입력 차원으로 변환하는 데 사용됩니다.
if bias: self.b_q = np.random.rand(num_hiddens) self.b_k = np.random.rand(num_hiddens) self.b_v = np.random.rand(num_hiddens) self.b_o = np.random.rand(num_hiddens) else: self.b_q = self.b_k = self.b_v = self.b_o = np.zeros(num_hiddens)
Python
복사
마지막으로 쿼리, 키, 값, 출력 변환을 위한 바이어스 벡터를 초기화합니다. bias 매개변수가 True로 설정되면 이 바이어스는 무작위로 초기화됩니다. 그렇지 않으면 0으로 설정됩니다.
•
b_q: 쿼리 변환의 바이어스.
•
b_k: 키 변환의 바이어스.
•
b_v: 값 변환의 바이어스.
•
b_o: 출력 변환의 바이어스.
바이어스의 차원은 히든 유닛 수와 같습니다.
이러한 가중치와 바이어스를 설정함으로써 각 어텐션 헤드가 입력 데이터의 다른 부분에 독립적으로 집중할 수 있게 됩니다.

3.2: 데이터 준비하고 변환하기

다음으로, 다중 헤드 어텐션을 위한 데이터를 준비하고 변환하는 메서드를 정의합니다. 먼저 transpose_qkv 메서드를 살펴보겠습니다.
def transpose_qkv(self, X): X = X.reshape(X.shape[0], X.shape[1], self.num_heads, -1) X = X.transpose(0, 2, 1, 3) return X.reshape(-1, X.shape[2], X.shape[3])
Python
복사
이 메서드는 다중 헤드 어텐션을 위해 입력 데이터를 재구성하고 변환하는 역할을 합니다.
# def transpose_qkv(self, X): X = X.reshape(X.shape[0], X.shape[1], self.num_heads, -1) # X = X.transpose(0, 2, 1, 3) # return X.reshape(-1, X.shape[2], X.shape[3])
Python
복사
입력 텐서 X를 네 차원으로 재구성합니다.
•
X.shape[0]: 배치 크기.
•
X.shape[1]: 시퀀스 길이(입력 시퀀스의 위치 수).
•
self.num_heads: 어텐션 헤드 수.
•
-1: 마지막 차원의 크기를 자동으로 추론하여 총 요소 수를 동일하게 유지합니다.
# def transpose_qkv(self, X): # X = X.reshape(X.shape[0], X.shape[1], self.num_heads, -1) X = X.transpose(0, 2, 1, 3) # return X.reshape(-1, X.shape[2], X.shape[3])
Python
복사
•
텐서의 차원을 (배치 크기, 헤드 수, 시퀀스 길이, 헤드별 깊이)로 재배열합니다.
이 재배열은 각 어텐션 헤드가 입력 시퀀스의 일부를 독립적으로 처리할 수 있게 합니다.
# def transpose_qkv(self, X): # X = X.reshape(X.shape[0], X.shape[1], self.num_heads, -1) # X = X.transpose(0, 2, 1, 3) return X.reshape(-1, X.shape[2], X.shape[3])
Python
복사
•
마지막으로 배치 및 헤드 차원을 단일 차원으로 평탄화하여 텐서를 (배치 크기 * 헤드 수, 시퀀스 길이, 헤드별 깊이) 형태로 만듭니다.
이렇게 하면 transpose_qkv는 입력 데이터가 여러 헤드 간에 올바르게 분할되도록 하여 각 헤드가 데이터를 처리하는 데 적절한 차원을 갖도록 합니다.
다음은 transpose_output 메서드입니다.
def transpose_output(self, X): X = X.reshape(-1, self.num_heads, X.shape[1], X.shape[2]) X = X.transpose(0, 2, 1, 3) return X.reshape(X.shape[0], X.shape[1], -1)
Python
복사
이 메서드는 transpose_qkv에 의해 수행된 변환을 역전하여 모든 헤드의 출력을 원래 형태로 결합합니다.

3.3: Scaled Dot Product Attention

우리의 행렬을 변환한 후, 스케일된 점곱 어텐션 메커니즘으로 처리할 수 있습니다. 이는 모델이 입력 시퀀스의 다른 부분에 다양한 중요도로 집중할 수 있게 합니다.
def scaled_dot_product_attention(self, Q, K, V, valid_lens): d_k = Q.shape[-1] scores = np.matmul(Q, K.transpose(0, 2, 1)) / np.sqrt(d_k) if valid_lens is not None: mask = np.arange(scores.shape[-1]) < valid_lens[:, None] scores = np.where(mask[:, None, :], scores, -np.inf) attention_weights = np.exp(scores - np.max(scores, axis=-1, keepdims=True)) attention_weights /= attention_weights.sum(axis=-1, keepdims=True) return np.matmul(attention_weights, V)
Python
복사
이 메서드의 입력은 쿼리(Q), 키(K), 값(V) 행렬입니다. 이 행렬들은 선형 변환을 통해 입력 데이터에서 파생됩니다.
def scaled_dot_product_attention(self, Q, K, V, valid_lens): d_k = Q.shape[-1] # scores = np.matmul(Q, K.transpose(0, 2, 1)) / np.sqrt(d_k) # if valid_lens is not None: # mask = np.arange(scores.shape[-1]) < valid_lens[:, None] # scores = np.where(mask[:, None, :], scores, -np.inf) # attention_weights = np.exp(scores - np.max(scores, axis=-1, keepdims=True)) # attention_weights /= attention_weights.sum(axis=-1, keepdims=True) # return np.matmul(attention_weights, V)
Python
복사
•
여기서 쿼리 행렬 Q의 마지막 차원에서 키 벡터의 차원 d_k를 추출합니다. 이 값은 어텐션 점수를 스케일링하는 데 사용됩니다.
# def scaled_dot_product_attention(self, Q, K, V, valid_lens): # d_k = Q.shape[-1] scores = np.matmul(Q, K.transpose(0, 2, 1)) / np.sqrt(d_k) # if valid_lens is not None: # mask = np.arange(scores.shape[-1]) < valid_lens[:, None] # scores = np.where(mask[:, None, :], scores, -np.inf) # attention_weights = np.exp(scores - np.max(scores, axis=-1, keepdims=True)) # attention_weights /= attention_weights.sum(axis=-1, keepdims=True) # return np.matmul(attention_weights, V)
Python
복사
•
Q와 K의 전치 행렬을 행렬 곱셈하여 어텐션 점수를 계산합니다.
# def scaled_dot_product_attention(self, Q, K, V, valid_lens): # d_k = Q.shape[-1] # scores = np.matmul(Q, K.transpose(0, 2, 1)) / np.sqrt(d_k) if valid_lens is not None: mask = np.arange(scores.shape[-1]) < valid_lens[:, None] scores = np.where(mask[:, None, :], scores, -np.inf) attention_weights = np.exp(scores - np.max(scores, axis=-1, keepdims=True)) attention_weights /= attention_weights.sum(axis=-1, keepdims=True) return np.matmul(attention_weights, V)
Python
복사
•
그런 다음 d_k의 제곱근으로 점수를 스케일링합니다. 이 스케일링은 점수가 너무 커지는 것을 방지하여 소프트맥스 계산 중 문제를 방지합니다.

3.4: Forward Method

다음으로, 입력 데이터를 다중 헤드 어텐션 메커니즘을 통해 처리하는 순전파 메서드를 정의합니다. 이 메서드는 입력 데이터를 변환하여 여러 헤드의 출력을 결합하는 전체 다중 헤드 어텐션 프로세스를 조율하는 데 중요합니다.
def forward(self, queries, keys, values, valid_lens): queries = self.transpose_qkv(np.dot(queries, self.W_q) + self.b_q) keys = self.transpose_qkv(np.dot(keys, self.W_k) + self.b_k) values = self.transpose_qkv(np.dot(values, self.W_v) + self.b_v) if valid_lens is not None: valid_lens = np.repeat(valid_lens, self.num_heads, axis=0) output = self.scaled_dot_product_attention(queries, keys, values, valid_lens) output_concat = self.transpose_output(output) return np.dot(output_concat, self.W_o) + self.b_o
Python
복사
다음은 forward 메서드를 단계별로 설명한 것입니다:
# def forward(self, queries, keys, values, valid_lens): queries = self.transpose_qkv(np.dot(queries, self.W_q) + self.b_q) keys = self.transpose_qkv(np.dot(keys, self.W_k) + self.b_k) values = self.transpose_qkv(np.dot(values, self.W_v) + self.b_v) # if valid_lens is not None: # valid_lens = np.repeat(valid_lens, self.num_heads, axis=0) # output = self.scaled_dot_product_attention(queries, keys, values, valid_lens) # output_concat = self.transpose_output(output) # return np.dot(output_concat, self.W_o) + self.b_o
Python
복사
먼저, 입력 쿼리, 키, 값은 학습된 가중치 행렬(W_q, W_k, W_v)과 바이어스(b_q, b_k, b_v)를 사용하여 각각의 하위 공간으로 투영됩니다. 이는 가중치 행렬과의 행렬 곱셈을 수행하고 바이어스를 추가하여 이루어집니다. 결과는 transpose_qkv 메서드를 사용하여 다중 헤드 어텐션에 맞게 변환됩니다. 이 메서드는 데이터를 재구성하고 변환하여 각 헤드가 입력을 독립적으로 처리할 수 있게 합니다.
쿼리, 키, 값은 변환된 입력으로, 이제 다중 헤드 어텐션을 준비합니다.
#def forward(self, queries, keys, values, valid_lens): # queries = self.transpose_qkv(np.dot(queries, self.W_q) + self.b_q) # keys = self.transpose_qkv(np.dot(keys, self.W_k) + self.b_k) # values = self.transpose_qkv(np.dot(values, self.W_v) + self.b_v) if valid_lens is not None: valid_lens = np.repeat(valid_lens, self.num_heads, axis=0) # output = self.scaled_dot_product_attention(queries, keys, values, valid_lens) # output_concat = self.transpose_output(output) # return np.dot(output_concat, self.W_o) + self.b_o
Python
복사
valid_lens(유효 길이)가 제공되면, 각 헤드에 대해 반복됩니다. 이는 각 어텐션 헤드에 적절한 마스크가 생성되어 모델이 시퀀스 내 유효한 위치에만 집중할 수 있게 합니다.
#def forward(self, queries, keys, values, valid_lens): # queries = self.transpose_qkv(np.dot(queries, self.W_q) + self.b_q) # keys = self.transpose_qkv(np.dot(keys, self.W_k) + self.b_k) # values = self.transpose_qkv(np.dot(values, self.W_v) + self.b_v) # if valid_lens is not None: # valid_lens = np.repeat(valid_lens, self.num_heads, axis=0) output = self.scaled_dot_product_attention(queries, keys, values, valid_lens) # output_concat = self.transpose_output(output) # return np.dot(output_concat, self.W_o) + self.b_o
Python
복사
그런 다음, 변환된 쿼리, 키, 값, 반복된 유효 길이를 사용하여 scaled_dot_product_attention 메서드를 호출합니다. 이 함수는 어텐션 점수를 계산하고, 소프트맥스 함수를 적용하여 어텐션 가중치를 얻은 다음, 가중치 합을 계산하여 각 헤드의 어텐션 출력을 생성합니다.
#def forward(self, queries, keys, values, valid_lens): # queries = self.transpose_qkv(np.dot(queries, self.W_q) + self.b_q) # keys = self.transpose_qkv(np.dot(keys, self.W_k) + self.b_k) # values = self.transpose_qkv(np.dot(values, self.W_v) + self.b_v) # if valid_lens is not None: # valid_lens = np.repeat(valid_lens, self.num_heads, axis=0) # output = self.scaled_dot_product_attention(queries, keys, values, valid_lens) output_concat = self.transpose_output(output) return np.dot(output_concat, self.W_o) + self.b_o
Python
복사
모든 헤드의 어텐션 출력을 얻은 후, transpose_output을 사용하여 특징 차원에 따라 이 출력을 결합합니다. 이 메서드는 초기 변환을 역전하여 모든 헤드의 출력을 단일 표현으로 결합합니다. 결합된 출력은 최종 선형 변환(W_o와 b_o)을 사용하여 원래 입력 차원으로 다시 변환됩니다.

3.5: 클래스 테스트

마지막으로, 몇 가지 샘플 데이터를 사용하여 클래스를 테스트합니다. 다음은 그 방법입니다:
# Define dimensions and initialize multi-head attention num_hiddens, num_heads = 100, 5 attention = MultiHeadAttention(num_hiddens, num_heads, dropout=0.5, bias=False)
Python
복사
다중 헤드 어텐션 클래스를 100개의 히든 유닛과 5개의 어텐션 헤드로 초기화합니다. 이는 다중 헤드 어텐션 메커니즘에 필요한 매개변수와 가중치 행렬을 설정합니다.
# Define sample data batch_size, num_queries, num_kvpairs = 2, 4, 6 valid_lens = np.array([3, 2]) X = np.random.rand(batch_size, num_queries, num_hiddens) # Use random data to simulate input queries Y = np.random.rand(batch_size, num_kvpairs, num_hiddens) # Use random data to simulate key-value pairs
Python
복사
입력 쿼리(X)와 키-값 쌍(Y)을 시뮬레이션하기 위해 임의의 데이터를 생성합니다. 배치 크기는 2, 쿼리 수는 4, 키-값 쌍의 수는 6입니다. 시퀀스 내 유효한 위치를 나타내는 유효 길이(valid_lens)도 정의합니다.
# Apply multi-head attention output = attention.forward(X, Y, Y, valid_lens)
Python
복사
샘플 데이터를 forward 메서드를 사용하여 다중 헤드 어텐션 메커니즘을 통해 전달합니다. 이는 입력 쿼리, 키, 값을 처리하여 다중 헤드 어텐션 계산을 적용합니다.
print("Output shape:", output.shape) # Output should be: (2, 4, 100) print("Output data:", output)
Python
복사
출력의 형태와 내용을 출력합니다. 예상 출력 형태는 원래 입력 차원과 일치합니다. 다중 헤드 어텐션을 계산한 후 출력 데이터를 출력합니다.
이제 다중 헤드 어텐션 메커니즘이 어떻게 작동하는지 이해했으므로, 이를 변경해 보세요. 예를 들어, 헤드 수를 변경하거나 다중 헤드 어텐션 전후에 여러 FFN을 추가해 보세요. 또한, 이를 기계 번역 작업에 구현하여 작동을 확인해 보세요.

4. 결론

트랜스포머는 자기 어텐션 메커니즘을 사용하여 입력 시퀀스를 병렬 처리함으로써 특히 NLP에서 딥러닝을 혁신했습니다. 이 접근 방식은 계산 속도를 높일 뿐만 아니라 기존의 순환 신경망보다 장기 의존성을 더 효과적으로 처리합니다.
이번 글에서는 트랜스포머의 다중 헤드 어텐션에 대해 수학적 이론부터 실제 코드 구현까지 포괄적으로 이해했습니다. 현재는 다중 헤드 어텐션의 출력만으로는 많은 것을 할 수 없지만, 트랜스포머 아키텍처에서 이들이 중요한 역할을 한다는 것을 곧 알게 될 것입니다. 앞으로의 글에서는 트랜스포머 아키텍처의 나머지 구성 요소를 탐구하여 이 강력한 모델에 대한 깊은 통찰을 제공할 예정입니다.

5. References