정렬 알고리즘 비교: 거품, 선택, 삽입, 기수, 병합, 퀵, 힙 정렬

TL; DR:

들어가며

거품 정렬 (Bubble Sort)

선택 정렬 (Selection Sort)

삽입 정렬 (Insertion Sort)

TL; DR:

credit: https://www.toptal.com/developers/sorting-algorithms

정렬 알고리즘	평균 시간 복잡도	최악 시간 복잡도	최선 시간 복잡도	공간 복잡도	특징	적합한 경우	Stable
거품 정렬 (Bubble Sort)	$\mathcal{O}(n^2)$	$\mathcal{O}(n^2)$	$\mathcal{O}(n)$	$\mathcal{O}(1)$	간단하지만 비효율적	작은 데이터셋, 교육 목적	O
선택 정렬 (Selection Sort)	$\mathcal{O}(n^2)$	$\mathcal{O}(n^2)$	$\mathcal{O}(n^2)$	$\mathcal{O}(1)$	비교는 많지만 교환은 적음	작은 데이터셋	X
삽입 정렬 (Insertion Sort)	$\mathcal{O}(n^2)$	$\mathcal{O}(n^2)$	$\mathcal{O}(n)$	$\mathcal{O}(1)$	거의 정렬된 데이터에 효과적	거의 정렬된 데이터셋	O
기수 정렬 (Radix Sort)	$\mathcal{O}(nk)$	$\mathcal{O}(nk)$	$\mathcal{O}(nk)$	보조 공간 필요	숫자 및 고정 길이 데이터에 적합	숫자 정렬	O
병합 정렬 (Merge Sort)	$\mathcal{O}(n\log{n})$	$\mathcal{O}(n\log{n})$	$\mathcal{O}(n\log{n})$	$\mathcal{O}(n)$	안정적, 병합에 추가 공간 필요	큰 데이터셋, 안정성 필요할 때	O
퀵 정렬 (Quick Sort)	$\mathcal{O}(n\log{n})$	$\mathcal{O}(n^2)$	$\mathcal{O}(n\log{n})$	$\mathcal{O}(n\log{n})$	평균적으로 빠르지만 최악의 경우 주의 필요	일반적인 정렬, 큰 데이터셋	X
힙 정렬 (Heap Sort)	$\mathcal{O}(n\log{n})$	$\mathcal{O}(n\log{n})$	$\mathcal{O}(n\log{n})$	$\mathcal{O}(1)$	공간 효율적, 제자리 정렬	메모리 효율성을 고려할 때	X

들어가며

정렬 알고리즘은 컴퓨터 과학의 기본적인 기술로, 데이터를 특정 순서로 재배열하는 데 사용됩니다.

정렬 알고리즘의 효율성은 일반적으로 시간 복잡도, 공간 복잡도, 안정성 등의 요소에 따라 평가됩니다.

이 글에서는 다양한 정렬 알고리즘의 개요와 시간 복잡도, 공간 복잡도를 비교해 보겠습니다.

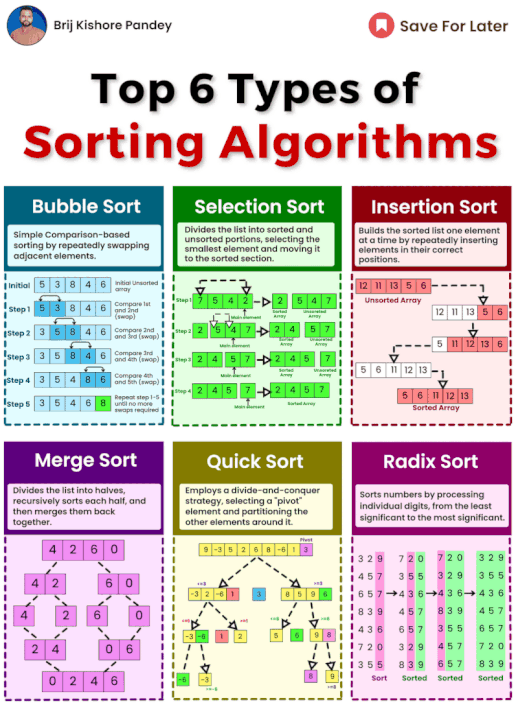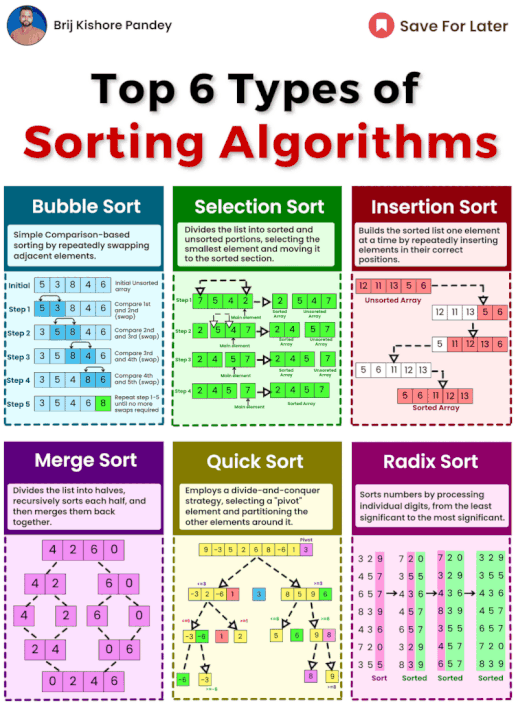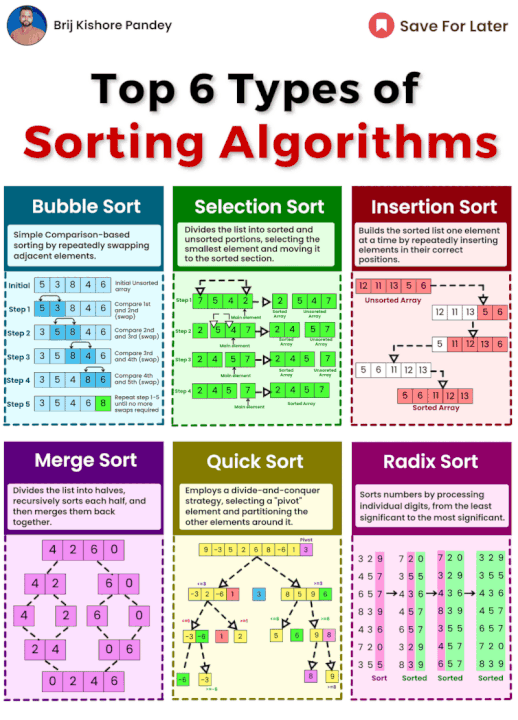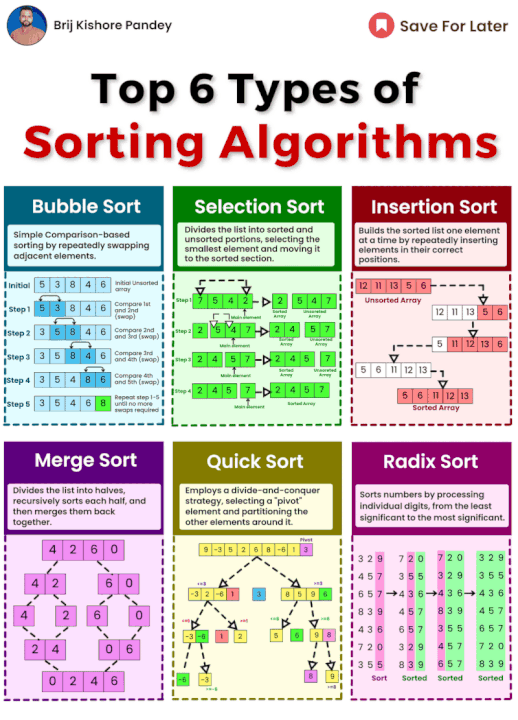
거품 정렬 (Bubble Sort)

•

리스트를 여러 번 반복하며 인접한 요소를 비교하고, 잘못된 순서에 있으면 교환합니다. 

•

리스트가 정렬될 때까지 이 과정을 반복합니다.

•

의사 코드:

for i from 0 to n-1
    for j from 0 to n-i-2
        if arr[j] > arr[j+1]
            swap arr[j] and arr[j+1]
JavaScript
복사

•

적합한 경우: 

◦

교육 목적으로 알고리즘의 기본 개념을 설명할 때 사용됩니다. 

◦

코드가 간단하고 이해하기 쉬워 기본적인 정렬 개념을 배우는 데 적합합니다.

선택 정렬 (Selection Sort)

•

입력 데이터를 정렬된 부분과 미정렬된 부분으로 나눕니다. 

•

미정렬된 부분에서 가장 작은(또는 큰) 요소를 찾아 정렬된 부분으로 이동시킵니다.

•

의사 코드:

for i from 0 to n-1
    min_index = i
    for j from i+1 to n-1
        if arr[j] < arr[min_index]
            min_index = j
    swap arr[i] and arr[min_index]
JavaScript
복사

•

적합한 경우: 

◦

코드의 단순함이 필요하거나 데이터셋이 작을 때. 

◦

교환 횟수가 적어야 하는 상황에서 유리할 수 있습니다.

삽입 정렬 (Insertion Sort)

•

정렬된 배열을 하나씩 확장하며 최종 배열을 구축합니다. 

•

작은 데이터셋에는 효율적입니다.

•

의사 코드:

for i from 1 to n-1
    key = arr[i]
    j = i - 1
    while j >= 0 and arr[j] > key
        arr[j + 1] = arr[j]
        j = j - 1
    arr[j + 1] = key
JavaScript
복사

•

적합한 경우: 

◦

데이터가 거의 정렬된 상태이거나, 실시간으로 정렬된 결과가 필요한 경우. 

◦

구현이 간단하고 효율적이어서 짧은 리스트에 적합합니다.

기수 정렬 (Radix Sort)

•

숫자나 고정된 길이의 문자열을 정렬하는 데 적합합니다. 가장 낮은 자릿수부터 가장 높은 자릿수까지 각 자릿수를 기준으로 정렬을 반복합니다.

•

Pseudo Code:

d = number of digits in the largest number
for i from 0 to d-1
    use stable sort (e.g., counting sort) on digit i
JavaScript
복사

•

적합한 경우: 

◦

숫자 데이터나 고정된 길이의 문자열처럼 데이터가 특정 형식에 맞춰져 있는 경우. 

◦

비교 기반 알고리즘보다 효율적인 정렬이 필요할 때.

병합 정렬 (Merge Sort)

•

분할 정복 알고리즘으로, 입력 배열을 반으로 나누어 재귀적으로 정렬한 후, 두 정렬된 반을 합칩니다.

•

의사 코드:

function mergeSort(arr)
    if length of arr > 1
        mid = length of arr / 2
        left = arr[0 to mid-1]
        right = arr[mid to end]
        mergeSort(left)
        mergeSort(right)
        merge(left, right, arr)

function merge(left, right, arr)
    i = j = k = 0
    while i < length of left and j < length of right
        if left[i] < right[j]
            arr[k] = left[i]
            i = i + 1
        else
            arr[k] = right[j]
            j = j + 1
        k = k + 1
    while i < length of left
        arr[k] = left[i]
        i = i + 1
        k = k + 1
    while j < length of right
        arr[k] = right[j]
        j = j + 1
        k = k + 1
JavaScript
복사

•

적합한 경우: 

◦

안정성이 중요하거나, 큰 데이터셋을 외부 정렬로 처리해야 할 때. 

◦

일관된 성능을 제공하며 안정적인 정렬이 필요할 때 사용됩니다.

퀵 정렬 (Quick Sort)

•

분할 정복 알고리즘으로, 배열을 선택된 피벗을 기준으로 두 부분으로 나누어 재귀적으로 정렬합니다.

•

의사 코드:

function quickSort(arr, low, high)
    if low < high
        pivotIndex = partition(arr, low, high)
        quickSort(arr, low, pivotIndex - 1)
        quickSort(arr, pivotIndex + 1, high)

function partition(arr, low, high)
    pivot = arr[high]
    i = low - 1
    for j from low to high - 1
        if arr[j] < pivot
            i = i + 1
            swap arr[i] and arr[j]
    swap arr[i + 1] and arr[high]
    return i + 1
JavaScript
복사

•

적합한 경우: 

◦

일반적인 데이터 정렬에서 가장 널리 사용되며, 평균적으로 빠른 성능이 필요할 때. 

◦

메모리 사용을 최소화하면서 큰 데이터셋을 정렬할 때 적합합니다.

힙 정렬 (Heap Sort)

•

이진 힙 데이터 구조를 기반으로 동작합니다. 

•

입력 배열을 최대 힙으로 구성하고, 가장 큰 요소를 반복적으로 추출하여 정렬된 배열을 만듭니다.

•

의사 코드:

function heapSort(arr)
    buildMaxHeap(arr)
    for i from length of arr - 1 to 1
        swap arr[0] and arr[i]
        heapify(arr, 0, i)

function buildMaxHeap(arr)
    for i from length of arr / 2 - 1 to 0
        heapify(arr, i, length of arr)

function heapify(arr, i, heapSize)
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2
    if left < heapSize and arr[left] > arr[largest]
        largest = left
    if right < heapSize and arr[right] > arr[largest]
        largest = right
    if largest != i
        swap arr[i] and arr[largest]
        heapify(arr, largest, heapSize)
JavaScript
복사

•

적합한 경우: 

◦

메모리 사용이 제한적이면서 안정성이 필요하지 않은 경우. 

◦

추가적인 메모리 공간 없이 효율적인 정렬이 필요할 때.

Sort의 속성

Stable Sort

만약 같은 값을 넣어 정렬을 하였을 때, 먼저 들어간 값이 반드시 앞쪽에 있음이 보장된다면, 우리는 이런 정렬을 "Stable"하다고 합니다.

모든 정렬 알고리즘은 Stable하지 않습니다. 즉 저런 상황에 놓인 경우, 아무 정렬 알고리즘이나 사용할 수 없습니다.

선택, 퀵, 힙은 Stable하지 않습니다.

In-place Sort

In-Place Sort란 추가적인 메모리 없이 정렬이 가능한 알고리즘을 뜻합니다.

병합, 기수는 In-place가 아닙니다.

Summary

credit: Brij kishore Pandey

이 포스트에서 다양한 정렬 알고리즘의 개요와 슈도코드, 적합한 사례를 살펴보았습니다.

•

거품 정렬은 단순하지만 효율성이 낮은 알고리즘이며

•

선택 정렬은 교환 횟수는 적지만 비교가 많아 느린 특성이 있습니다. 

•

삽입 정렬은 거의 정렬된 데이터에 효과적입니다. 

•

기수 정렬은 비교 기반이 아닌 알고리즘으로, 특정 숫자 데이터에 적합합니다.

•

병합 정렬은 큰 데이터셋에서 안정적이고 효율적이지만 추가 메모리가 필요합니다. 

•

퀵 정렬은 평균적으로 빠른 성능을 자랑하지만 피벗 선택에 따라 성능이 달라질 수 있습니다. 

•

힙 정렬은 메모리 효율성이 뛰어나지만, 안정성이 필요하지 않은 경우에 적합합니다.