Towards a Definition of Disentangled Representations
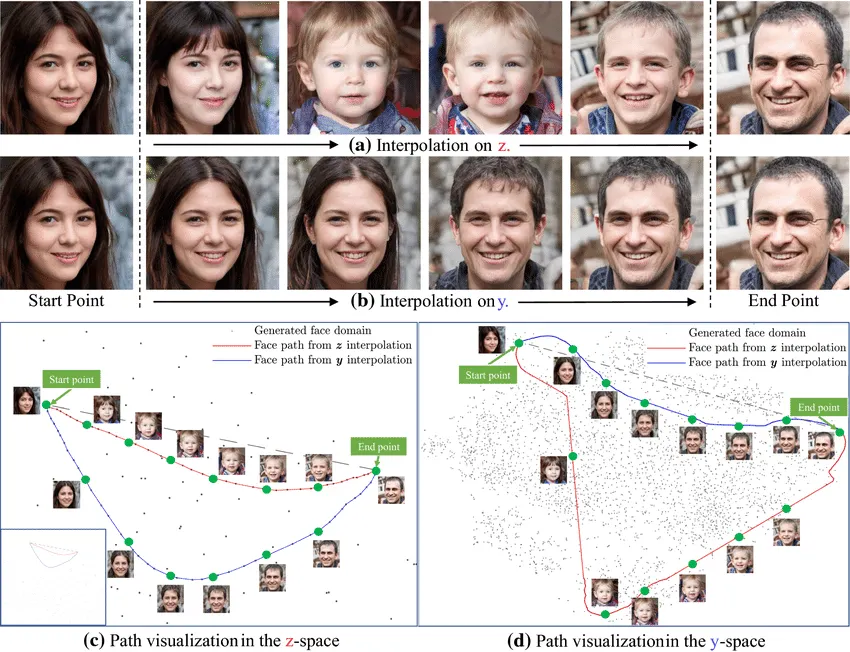
Image editing, Translation 분야에서 우리는 “Disentangle”이라는 표현을 자주 접합니다. 그리고 이 단어는 꽤 직관적입니다. latent representation에서 특정 요소를 분리해 내겠다는 뜻이겠죠? 하지만 이를 수학적으로 엄밀히 정의해볼 수 있을까요? 언제 Disentangle이 되었다고 말할 수 있을까요?
한번쯤 봤을 가장 유명한 일러스트레이션. 위쪽 그림은 Entangle된 상태, 아래 그림은 Disentangle된 상태. credit: zhu 2022
Disentangled Representations
먼저 Disentangled representation의 의미를 짚어보겠습니다.
Disentangled representations는 직관적인 의미에서 Neural Network가 학습하는 Latent Factors가 의미론적으로 의미가 있다는 것을 의미합니다.
예를 들어, 3D 장면에 객체가 있는 경우, Latent representation은 크기, 색상, 모양, 위치를 별도로 인코딩해야 합니다. 하지만, 이것은 모호한 개념입니다. 실제로 현재의 방법들은 매우 다양한 Inductive biases를 포함하고 있으며, 다양한 Metric을 만들어냈습니다. Uncorrelated Factors는 이해가 되지만, 이것이 전부일까요?
Disentanglement는 많은 사람들이 관심을 가지고 있지만 명확하게 표현할 수 없었던 모호한 개념이었습니다. Geometric Deep Learning의 기본을 공부하면서, Invariance, Equivariance, Symmetries의 개념이 Disentanglement를 생각하는 데 유용하다는 것을 알게 되었습니다. Higgins et al. (2018)은 Disentanglement를 Geometric Deep Learning 관점에서 접근합니다.
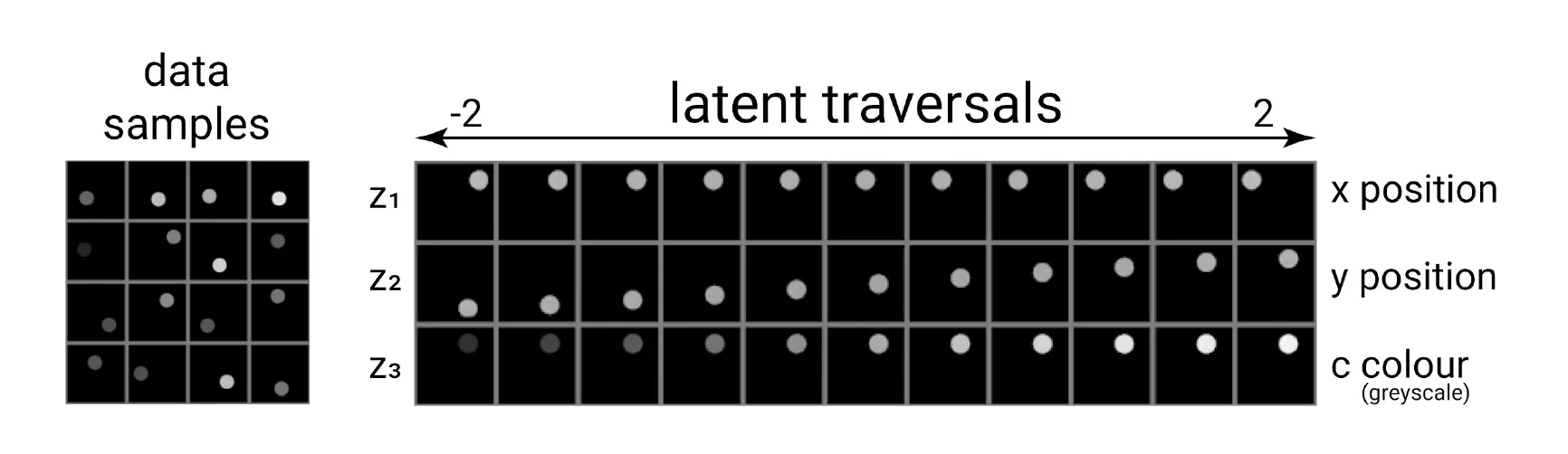
하지만 먼저, 우리는 단순히 의미론적으로 의미가 있는 Latents를 원한다고 말하는 것보다 더 구체적이어야 합니다. 시각적으로 예를 들어 보겠습니다. 2D 평면에 있는 그레이스케일 점들에 대해, 우리는 x, y 위치, 색상을 Latents로 가집니다.
Disentangled Representation의 속성
그렇다면, Disentangled Representation이 가져야 할 속성은 무엇일까요?
첫 번째 접근법은 DCI 점수에 의해 가이드됩니다. 이는 Disentangled (Modular), Complete (Compact), Informative (Explicit)한지 여부에 따라 의미론적으로 의미가 있는 Representations을 정량화합니다.
DCI 점수에서 Disentanglement는 좋은 이름이 아닙니다.
Representation이 Disentangled되려면 세 가지 구성 요소가 모두 필요하기 때문입니다.
그렇기 때문에, 이 포스트에서는 Modularity, Compactness, Explicitness를 사용하겠습니다.
1. Modular (Disentangled)
단일 Latent Dimension이 단일 속성을 인코딩하는지 여부를 측정합니다.
예시:
•
Latent Factor z₁이 변경될 때 오직 하나의 속성만 변경된다면 (예: 객체의 크기) 그것은 Modular합니다.
반례:
•
만약 z₁가 변경되면서 색상과 크기가 모두 변경된다면, 이는 Modular하지 않습니다.
•
z₁, z₂, z₃가 객체의 3D 위치를 인코딩한다고 할 때, 이는 Canonical Base에서는 그렇지만 여전히 Modular할까요? 나중에 다시 알아보겠습니다.
2. Compact (Complete)
속성이 단일 Latent Dimension에 의해 인코딩되는지 여부를 측정합니다.
예시:
•
Completeness는 특정 z₁가 변경될 때만 속성(예: 색상)이 변경되어야 함을 요구합니다.
•
의 모든 경우에 속성은 동일하게 유지되어야 합니다.
반례:
•
Completeness는 Modularity와 반대 방향으로 Reasoning을 합니다.
즉, Modularity는 z₁, z₂가 색상을 인코딩하는 경우에도 충족되지만, 이러한 Representation은 Compact하지 않습니다.
3. Explicit (Informative)
Linear Transformation을 통해 Representation에서 모든 속성의 값을 디코딩할 수 있는지 여부를 측정합니다.
저자에 따르면 이런 Explicitness는 가장 가장 중요한 요구사항입니다. 이 요구사항은 두가지 조건을 만족해야 합니다.
•
조건 1: Disentangled Representation은 모든 Latent Factors를 포착해야 합니다.
1.
조건 2: 이 정보는 선형적으로 디코딩 가능해야 합니다.
예시:
•
특정 모양, 크기, 위치, 방향을 가진 단일 객체의 3D 장면에서, 이런 모든 요소는 Latent Factors에 해당하며, 우리는 선형 변환을 적용하여 모든 정보를 추출할 수 있습니다.
•
즉, 선형변환 행렬 에 대하여 이 성립합니다.
•
이 여러 속성을 변경할 수 있지만, 우리는 Matrix 를 찾아 Modularity가 성립하는 Factors를 얻을 수 있습니다.
반례:
•
조건 1은 어떤 속성이 Latents에 인코딩되지 않은 경우 만족하지 않습니다.
•
조건 2는 가 성립하지 않는 경우 만족하지 않습니다.
(예: 에 비선형 매핑이 있는 경우)
Disentanglement에 대한 기하학적 접근
가장 먼저, 대칭 (symmetry)에 대한 정의를 떠올려보겠습니다.
객체의 대칭(symmetry)이란, 객체의 특정 속성을 불변 (invariant) 으로 유지하는 변환 (transformation)입니다.
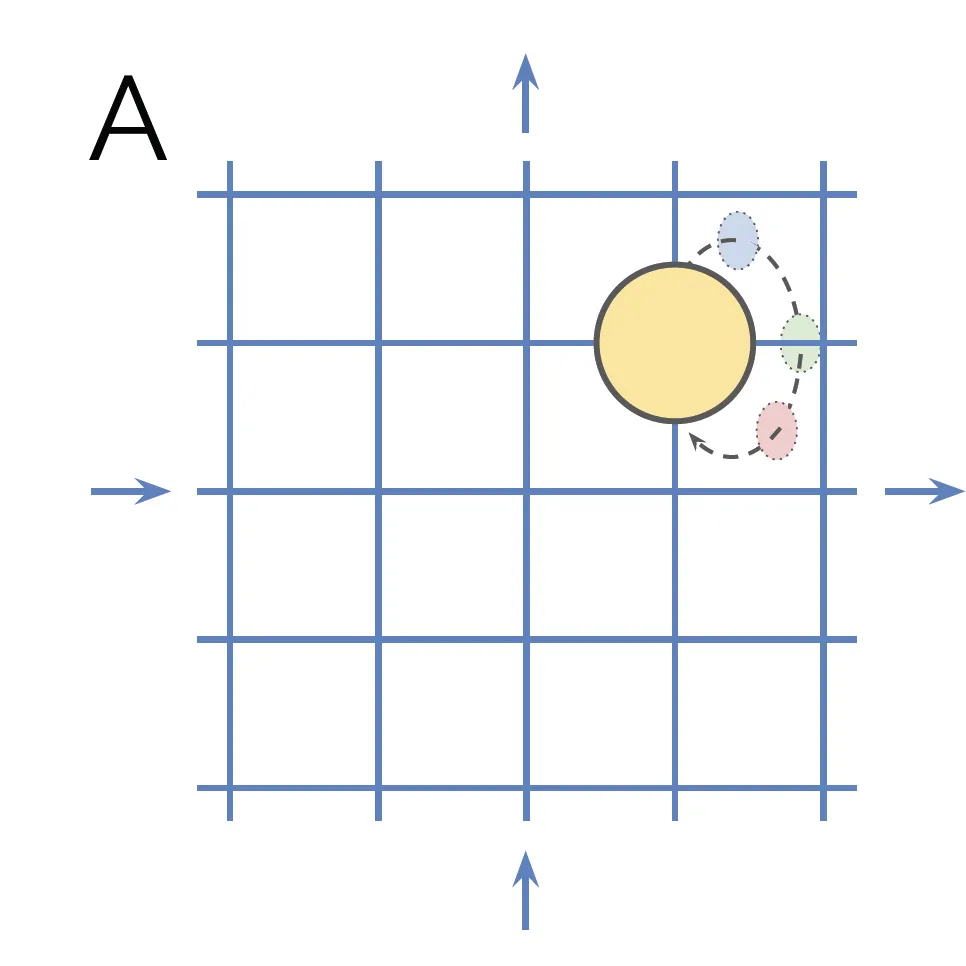
자, 여기서 예를 들어보겠습니다. 2차원 평면 위에 원이 존재하는 Grid World를 떠올려보겠습니다. 이 Grid World는 다음과 같은 속성을 가집니다.
1.
단일 객체
2.
네 가지 이동 방향
3.
단일 색상 구성 요소(색상)
4.
원형 구조
•
그리드의 오른쪽으로 벗어나면 객체가 왼쪽 가장자리 픽셀로 이동/색상 스펙트럼이 다시 시작됨.
•
Translation 및 색상 변경은 객체의 정체성을 변경하지 않습니다. 따라서 이는 symmetry이고, symmetry group 로 간주할 수 있습니다.
•
의 요소 는 데이터 공간에서 데이터 공간으로 매핑합니다: .
•
이는 이러한 변환을 Group Actions라고 볼 수 있습니다.
•
추가적으로, 우리는 G에서 Horizontal/Vertical Translation 및 색상 변경에 해당하는 하위 그룹을 만들 수 있습니다.
•
Disentangled Representation을 가지려면, 한 속성을 변경할 때 다른 속성은 일정하게 유지되어야 합니다.
(예를 들어 색상이 변경될 때 위치는 동일하게 유지되어야 함)
•
Geometric Deep Learning 관점에서 말한다면 번역하면, 다음과 같습니다.
Disentangled Group Action은 각 하위 그룹에 대한 요소로 분해되어야 하며, 해당 하위 그룹에만 영향을 미쳐야 합니다.
구성 요소는 G의 하위 그룹으로, 색상과 같은 요소를 변경할 때 우리는 하위 그룹 내에 남게 됩니다. 색상을 아무리 변경해도 위치가 변하지 않습니다.
첫 번째로 주목할 점은 여기에서
Disentangled Representation은 symmetry group G의 Disentangled Group Action으로 정의됩니다.
Latent space는 latent vector를 가지고 있으며, 그들의 선형 결합도 유효한 latent vector이기 때문에 vector representation을 의미합니다. 따라서 논문의 Disentanglement 정의는 다음과 같이 됩니다.
A vector representation is called a disentangled representation with respect to a particular decomposition of a symmetry group into subgroups, if it decomposes into independent subspaces, where each subspace is affected by the action of a single subgroup, and the actions of all other subgroups leave the subspace unaffected.
Vector Representation이 symetric group의 subgroup으로 분해되는 특정 분해에 대해, 독립된 subgroup으로 분해되고, 각각의 subspace의 action이 단일 subgroup에만 영향받는 경우, 이를 Disentangled Representation이라고 합니다.
이것은 정의가 sub group으로 G를 특정하게 분해하는 것에 따라 달라진다는 것을 의미합니다.
예를 들어, 두 개의 하위 그룹(하나는 위치, 하나는 색상)에만 해당하는 분해를 정의하면, 모델이 수평 및 수직 위치를 Disentangle할 수 있는지 여부는 중요하지 않습니다. 그리고 이것이 매우 중요한 점입니다.
This definition of disentanglement provides means to fine-tune the granularity w.r.t. which we require disentanglement.
이 Disentanglement 정의는 우리가 Disentanglement를 요구하는 세부 사항을 미세 조정할 수 있는 수단을 제공합니다.
실용적인 관점에서 이는 더 간단한 모델을 만들 수 있습니다. 특정 요소를 Disentangle하기 위해 모델 용량을 소비할 필요가 없기 때문입니다. 또한, 이는
There is no requirement on the dimensionality of the disentangled subspace.
Disentangled 하위 공간의 차원에 대한 요구 사항이 없다는 것을 의미합니다.
즉, 상관된 요소로 구성된 하위 그룹이 있더라도, 해당 그룹의 작용이 이 하위 공간에만 작용한다면 이는 Disentangled 상태입니다. 실제 세계에서 이러한 시나리오가 발생할 수 있습니다. 예를 들어, 키와 나이를 인코딩할 때 이들은 상관관계가 있습니다 (2미터의 아기는 없습니다).
이것이 충분하지 않을 때, 우리는 “하위 그룹의 기반에 대한 제한이 없다”는 점을 주목해야 합니다.
no restriction on the bases of the subgroups.
따라서 위치는 Cartesian Coordinate Axes로 설명될 필요가 없습니다.
또한, 모든 하위 그룹에 대해 그룹 작용에 선형성 제약을 부과하면, 우리는 선형 Disentangled Representation에 도달합니다(이것은 우리가 ρ 매트릭스를 가지고 있음을 의미합니다):
벡터 표현은 특정 하위 그룹으로 분해되는 대칭 그룹의 분해에 대해 Disentangled Representation이 되고, 모든 하위 그룹의 해당 하위 공간에 대한 작업이 선형인 경우, 이를 선형 Disentangled Representation이라고 합니다.
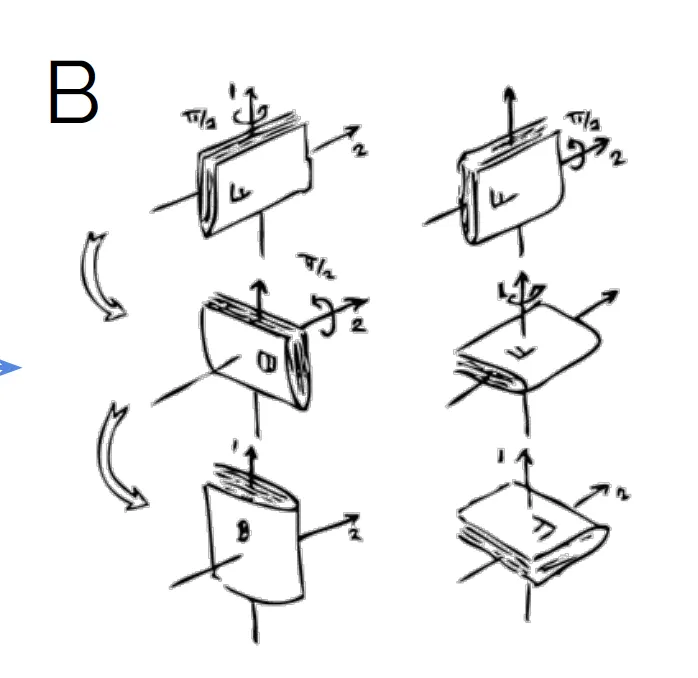
반례: 3D 회전
여기서 놀라운 반례는 3D 회전의 경우입니다. 즉, 이들은 교환법칙을 따르지 않으므로 (Higgins et al., 2018)의 정의에 따라 Disentangle될 수 없습니다. 즉, 교환법칙을 따르지 않기 때문에 그룹 작업(xx, yy, zz 축 주위 회전)이 다른 그룹 작업에 영향을 미칩니다. z축 주위를 회전하면 x축 주위 회전의 효과가 달라집니다. 따라서 그룹 작업은 Disentangle되지 않으며, 표현도 Disentangle되지 않습니다.
Conclusion
(Higgins et al., 2018)은 그룹 이론에 기반한 Disentanglement의 원칙적인 정의를 제공합니다. 이 주요 이점은 Disentangled Representations에 대해 명확하게 소통할 수 있게 해준다는 것입니다. 게다가, "데이터 생성 요소, 속성"과 같은 모호한 개념 대신에, 이들은 명확히 정의된 Group Actions에 대해 논의합니다.